矩阵
什么是矩阵

由m x n个数 组成的一个 m 行 n 列的数表,就是一个“矩阵”。用于存储数据信息。
矩阵于行列式有什么关系?
矩阵本质是一个数表,行列式本质是一个数。(我的理解:一个是数据解构,一个是数)
解构上类似:
矩阵的
行和列可以是任意的;行列式的
行和列必须相等的;只有矩阵的为
方阵(行和列相等)时,才具备一些行列式的特性。
同型矩阵
- 两个矩阵的行数、列数均相等。
相等矩阵
- 两个矩阵同型,并且元素均对应相等。
矩阵的运算
矩阵的加减运算
- 必须是同型矩阵才能相加减。
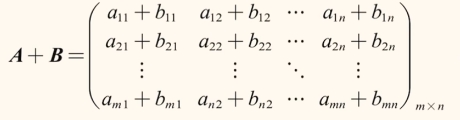
- 具有交换律:A+B=B+A
- 具有结合律:(A+B)+C=A+(B+C)
数与矩阵相乘

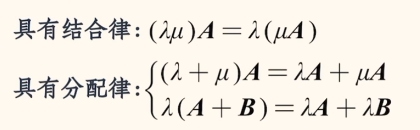
矩阵与矩阵相乘
- 左取
i行,右取j列,对应相乘再相加,构成新矩阵处在( i, j )位置的元素。能否相乘提看内标,结果看外标。
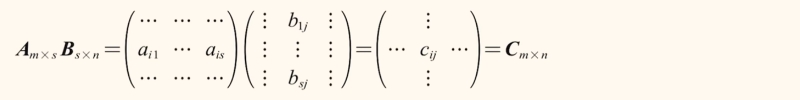
矩阵与矩阵的乘法运算性质
不具备交换律
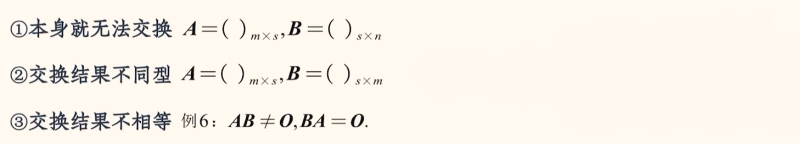
不具备消去律

具备结合律、左分配律、右分配律。
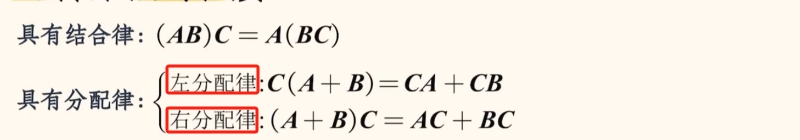
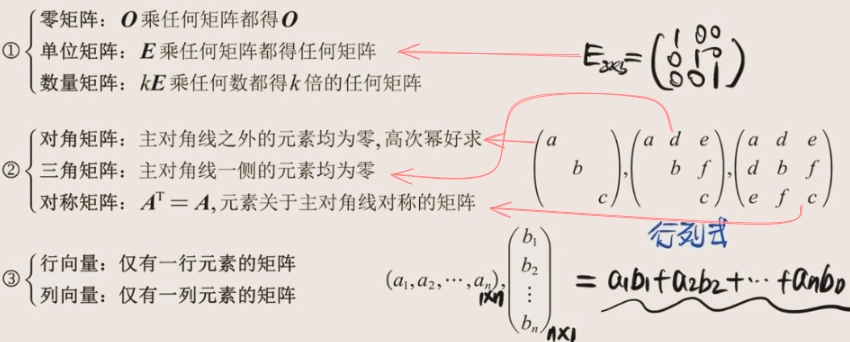
特殊矩阵
矩阵的转置
原来的矩阵
行变成列。矩阵转置的性质:

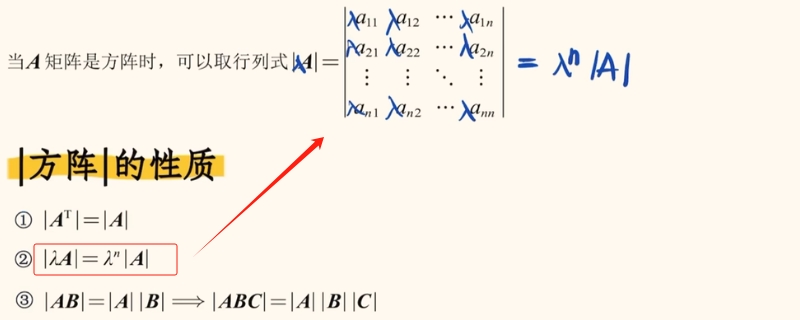
方正行列式
伴随矩阵
矩阵元素的代数余子式的转置;
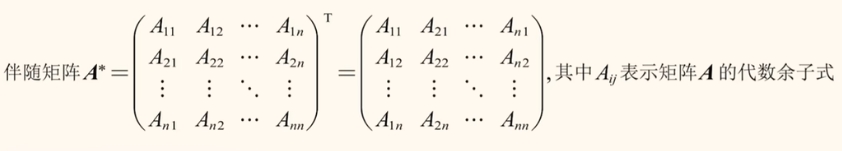
伴随矩阵的起源: 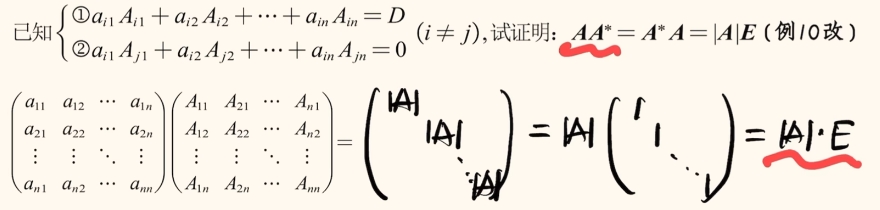
逆矩阵
回顾一下
倒数:在数的乘法中,若a≠0,则存在唯一的数b,使得ab=ba=1。
- 在矩阵的乘法中,若|A|≠0, 则存在唯一的矩阵B。使得AB=BA=E。则A可逆,矩阵B是A的逆矩阵,即B=A-1
逆矩阵的性质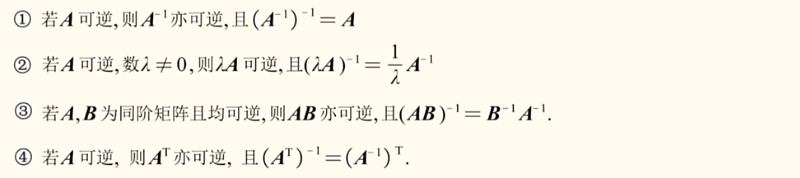
试题1: 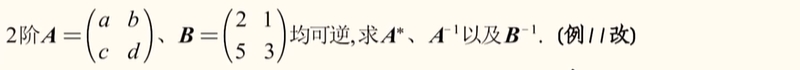
解析
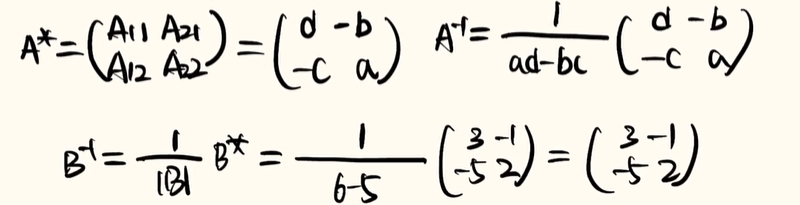
试题2: 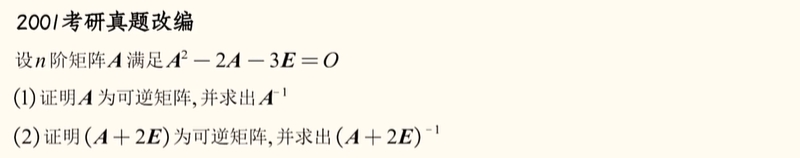
解析

试题3: 
解析
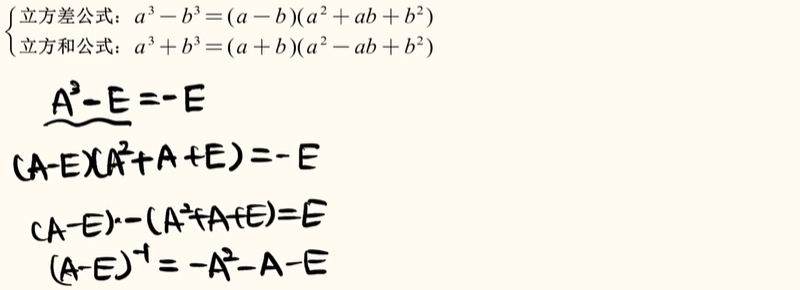
试题4: 
解析

逆矩阵与伴随矩阵
推论:A A* = A* A = |A| E