全排列 ​

3 元排列 ​

3元排列(有1.2.3三个数,不重不漏,按一定顺序排成一行,即是“一个"3元排列)

有多少种排列方式呢？

3元排总共 有 3! 种排列方式。

N 元排列 ​

n元排列(有1.2..n.共n个数,不重不漏,按一定顺序排成一行,即是"一个"n元排列)

n元排总共 有 n*(n-1)...*1 = n! 种排列方式。

逆序数 ​

若存在一个大数排在一个小数前面,则这一对数构成“一个逆序”，而逆序数,其实就是"逆序的总个数"。

逆序数不在乎个数、只在乎奇偶。

示例：

t（12...n） = 0

t（32514）= 5

奇偶排列 ​

• 逆序数为"奇"称为奇排列；

• 逆序数为"偶"称为偶排列；

兑换辆数，奇偶改变。

相邻兑换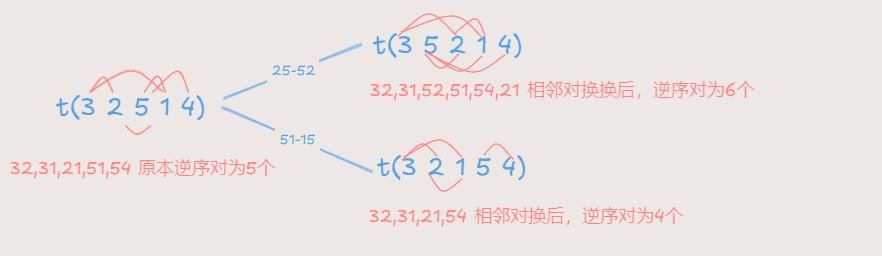

一组排列,若相邻两个数对换,则奇偶性发生改变。逆序数 +1 或 -1

任意兑换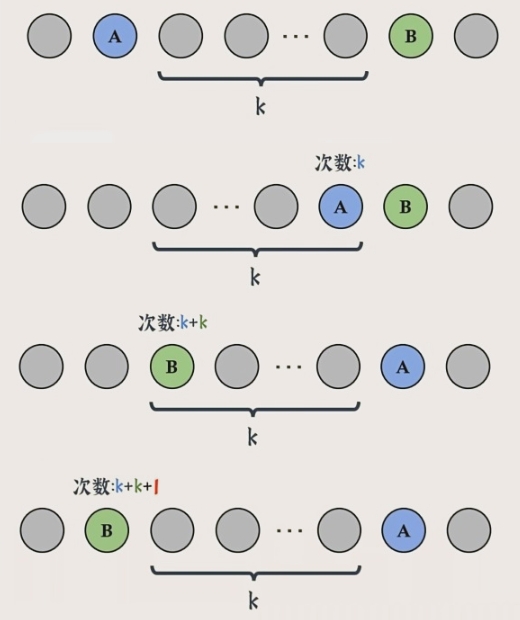

一组排列，任意两个数对换（2k+1为基数次）,则奇偶性必然发生改变。

试题