向量的线性组合与线性相关

向量组

若干同维数的向量a₁,a₂,……,a_n所组成的集合A，被称为向量组，记作:

A: a₁,a₂,……,a_n 或 A = { a₁,a₂,……,a_n }

线性组合：

\begin{matrix} c_{1}, c_{2}, . . ., c_{k} 为 常 数 ， v_{1}, v_{2}, . . ., v_{k} 为 R^{n} 中 的 向 量 \\ c_{1} v_{1} + c_{2} v_{2} + c_{k} v_{k} 为 向 量 v_{1}, v_{2}, . . ., v_{k} 的 线 性 组 合 。 \end{matrix}

线性表示：意思就是用线性组合来表示；

向量的全部线性组合所构成的向量集合就是它张成空间。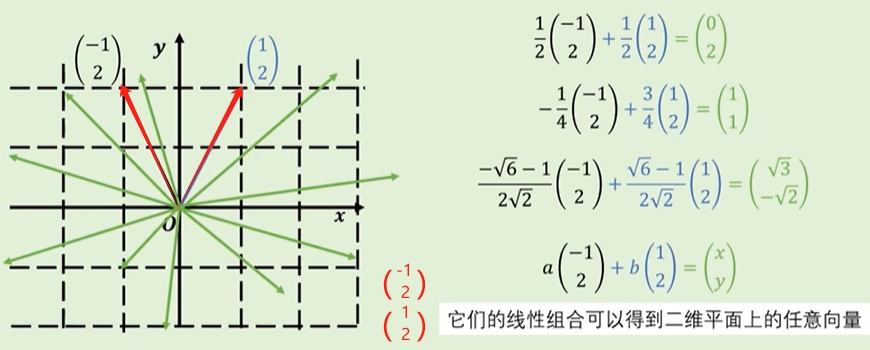

这个平面就它的张成空间

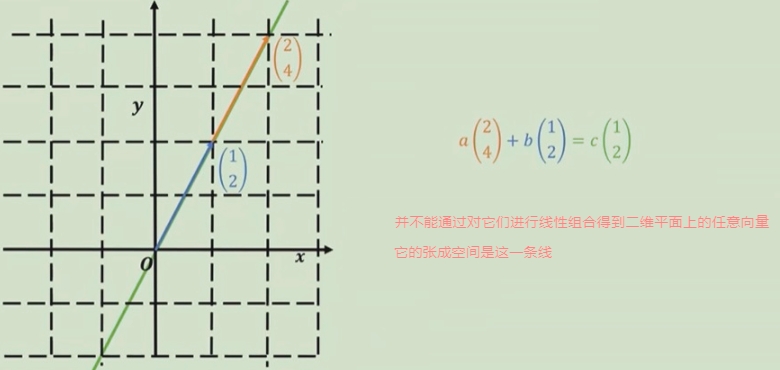
问题

为什么，有的向量的张成空间是一个平面，而有的张成空间是一条线？是因为的有向量是线性相关，有的向量是线性无关。

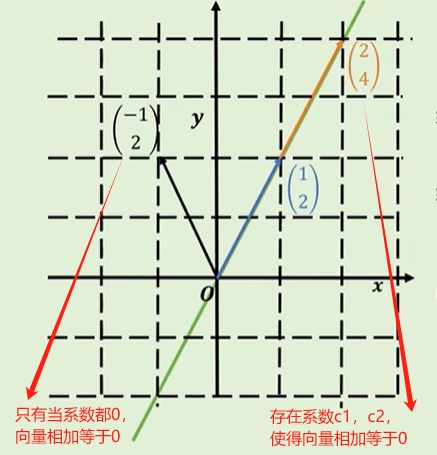
线性相关：

存在不全为零的系数时线性组合也为零（可通过系数拉伸向量可以使其相等）。

1 (\begin{matrix} 2 \\ 4 \end{matrix}) - 2 (\begin{matrix} 1 \\ 2 \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix})

线性无关：

n个向量组成的向量组的线性组合只在系数为零时为零（怎么拉伸都不可能相等）。

0 (\begin{matrix} - 1 \\ 2 \end{matrix}) + 0 (\begin{matrix} 1 \\ 2 \end{matrix}) = (\begin{matrix} 0 \\ 0 \end{matrix})

几何上的线性相关与线性无关

线性相关：这组向量里有多余的向量，把它去掉以后也不影响原有的张成空间。

线性无关：没有多余的向量，去掉任何一个都会影响原有的张成空间，每一个向量都代表了一个新的维度。

该向量组可以张成的空间的维度，用r来表示；

向量组里有多少个线性无关的向量，那么这个向量组的秩就是多少

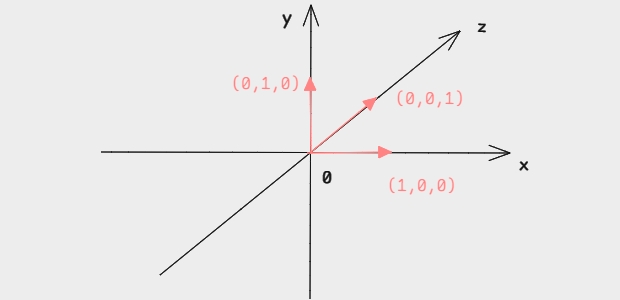
n个线性无关的向量可以通过线性组合张成一个n维空间---> 这n个线性无关的向量就是这个n维空间的 基。

标准的正交基 两两垂直，长度为1的基。

\hat{i} : x 轴 方 向 的 标 准 正 交 基

\hat{j} : y 轴 方 向 的 标 准 正 交 基

\hat{k} : z 轴 方 向 的 标 准 正 交 基

换基（线性变换）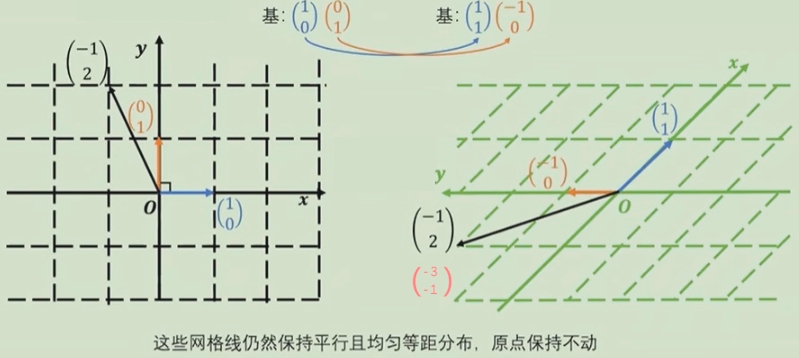

线性变换过程：

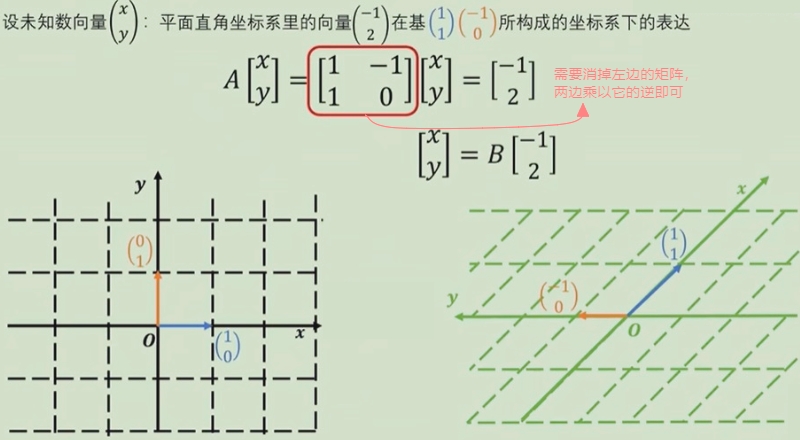
这里可以把矩阵理解成线性变换，逆矩阵理解成还原。