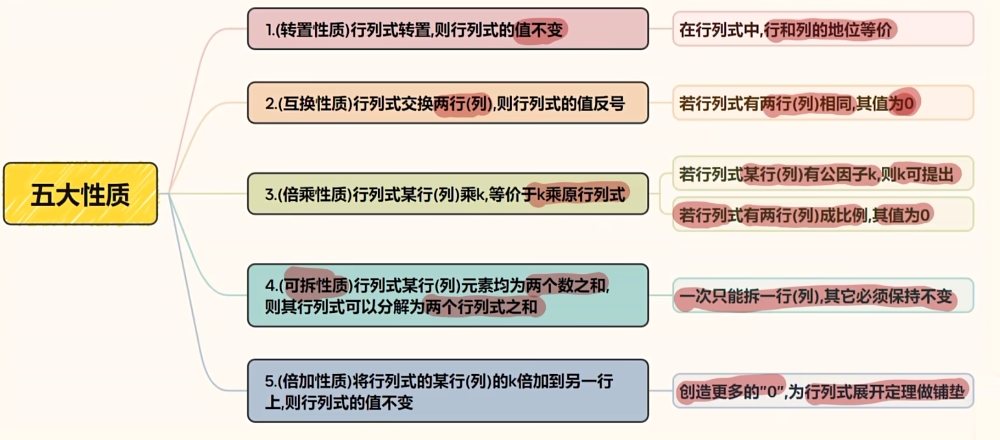
行列式的性质
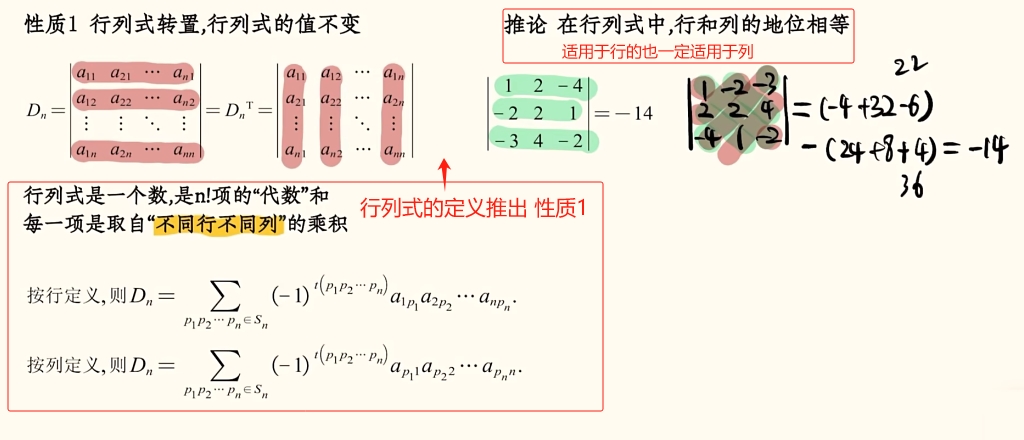
性质一:行列式转置
行列式转置,值不变;
D = D T,
行变为列;
推论:在行列式中,行和列的地位相等,适用于行的也一定适用于列;
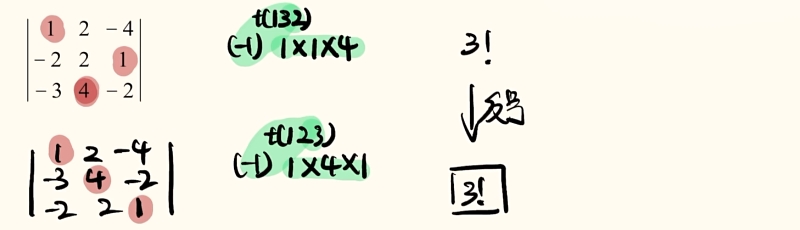
性质二:行列式的互换性质
- 行列式交换两行(或两列),其值取反号。
推论:若行列式在两行(列)相同,其值为0;

性质三:行列式的倍乘性质
- 行列式某行(列)乘k,等价于k乘原行列式;
推论一:若行列式某行(列)有公因子k,则k可以提出;
推论二:若行列式有两行(列)成比例,其值为0;

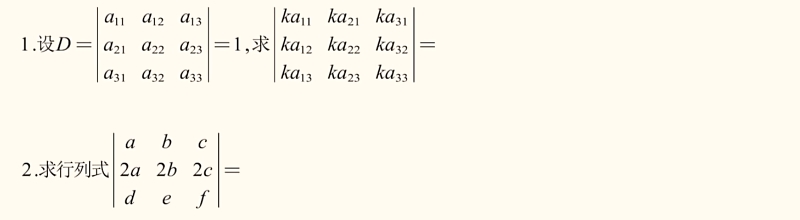
性质四:行列式的可拆性质
- 行列式某行(列)元素均为两个数之和,则行列式可以分解为两个行列式之和;
推论:单行(列)可拆性 一次只能拆一行(列)其它元素必须保持不变;
 试题:
试题: 
解析

性质五:行列式的倍加性质
- 将行列式的某行(列)的k倍加到另一行(列)上则行列式的值不变;
推论:创造更多的“0”,为行列式展开定理做铺垫; 
试题1: 
解析
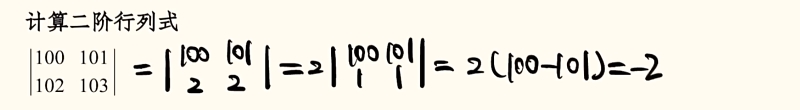
试题2: 
解析
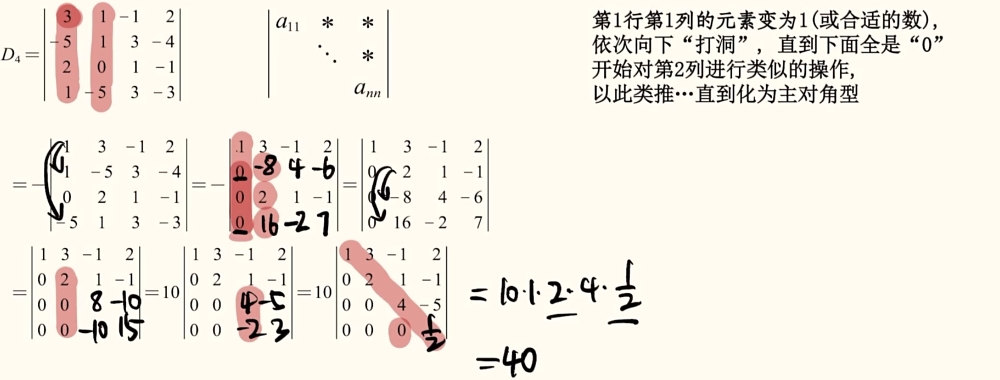
总结