行列式的展开
为什么要展开？
降阶行列式，要引入两个新的念：余子式、代数余子式。
余子式
- Mij(余子式)：选中一个元素后,直接删掉其所在的行列，剩余下来的元素按照原位置不变，再次构成的(n-1)阶行列式。
代数余子式
代数余子式 就是前面带着一个符号的余子式，就叫代数余子式。
这个符号由被选中元素的“位置”决定。
示例
行列式的展开定理
- 行列式 = 某一行(列)的“元素”与该行(列)的“代数余子式”对应相乘再相加。
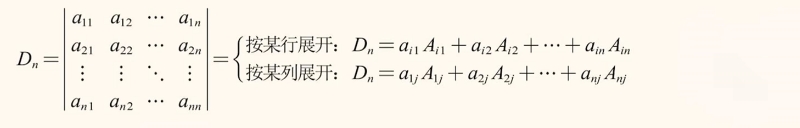
试题1： 
解析
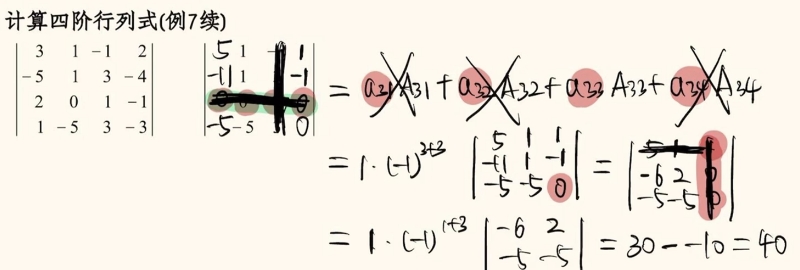
试题2： 
解析
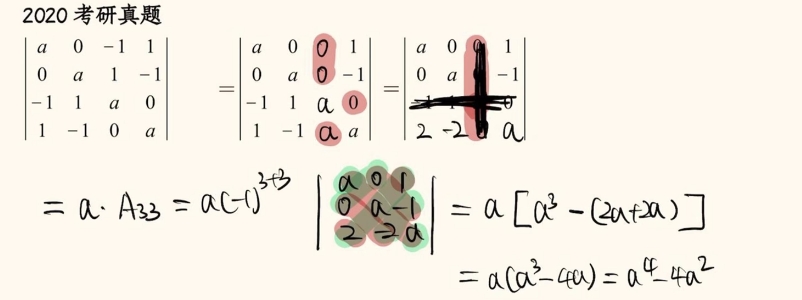
拓展--替换法则
替换法则起源
INFO
起源一： 
起源二： 
替换法则的基本原则
替换法则，代数余子式求和
试题1：
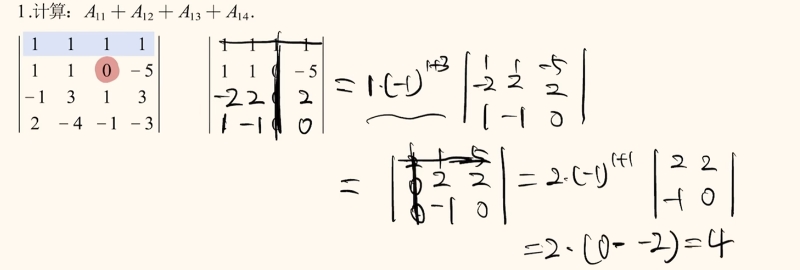
解析： 
解析：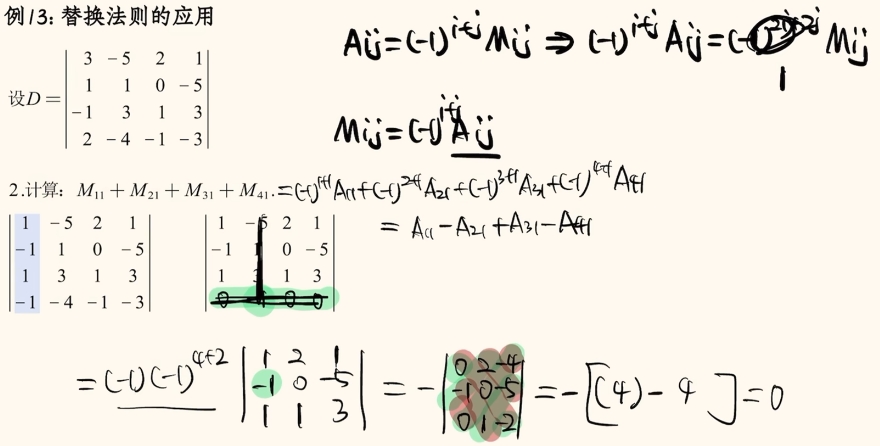 
试题2：
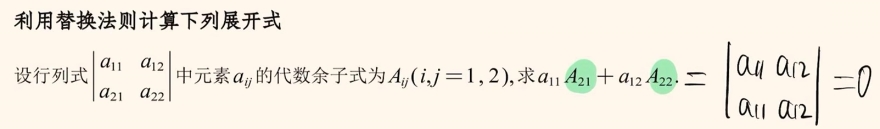
替换法则推论
试题1：
