向量的运算 ​

向量的加法 ​

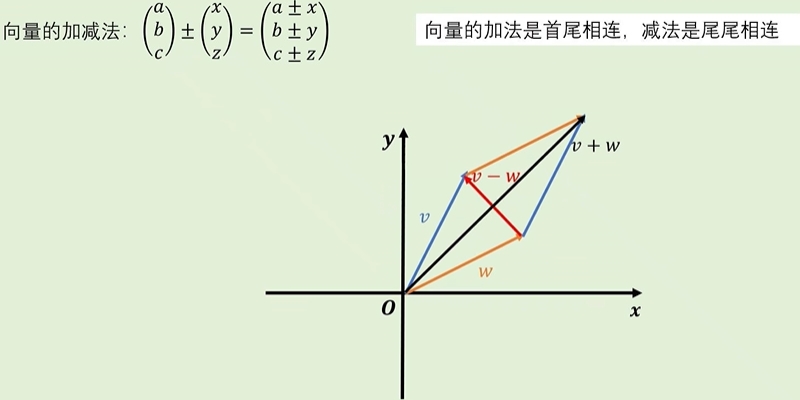
向量的加法：由向量v的终点处，做另一个向量w的起点，两个向量和就等于向量v的起点指向向量w的终点（主对角线）。

向量的减法：由向量v的终点处，做另一个向量-w的起点，两个向量和就等于向量v的起点指向向量-w的终点（副对角线，注意方向：向量的方向是减号后面向量的终点指向减号前面向量的终点）。

向量的数乘 ​

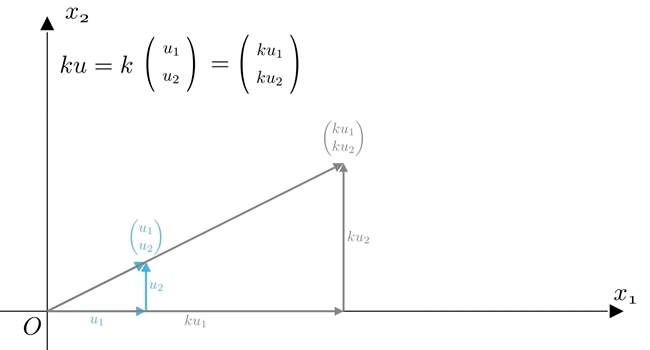
将各个分量，放大了k 倍。

它的几何含义：k < 0 时，反方向的伸缩，k > 0 时，同方向的伸缩

伸缩后的向量k与原向量u平行，因此可以借助数乘来定义平行:

若u和v满足u =kv,k∈R，则称u平行于v，记作u // v。

因为零向量0和任意向量u始终有0=0u，所以零向量与任意向量平行，也可以说零向量的方向任意。

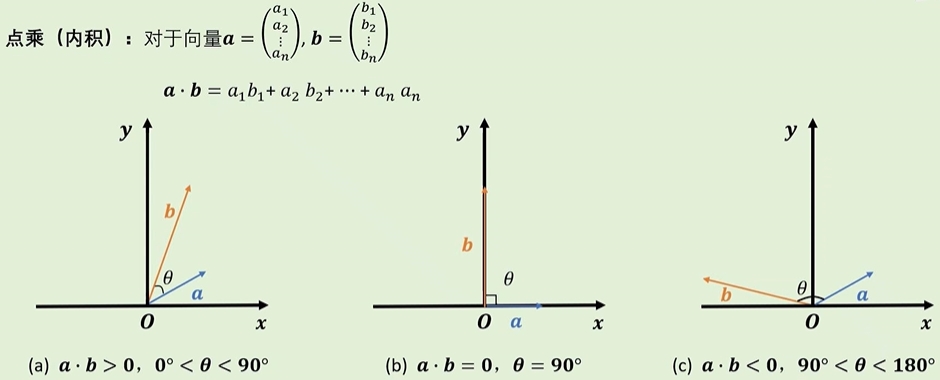
向量的点乘（内积） ​

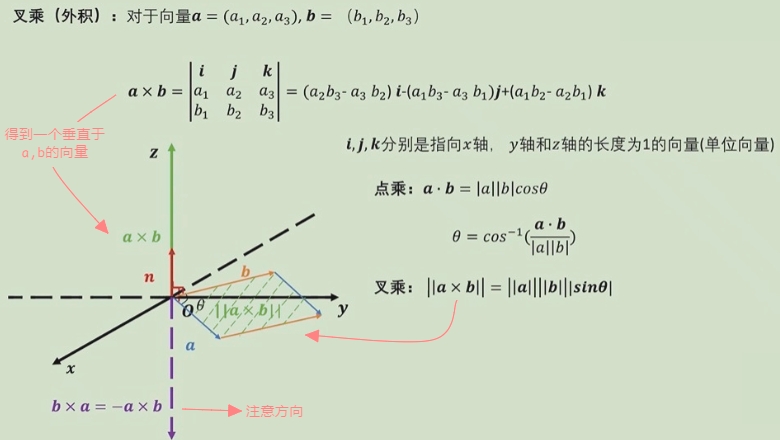
向量的叉乘（外积） ​