几何 ​

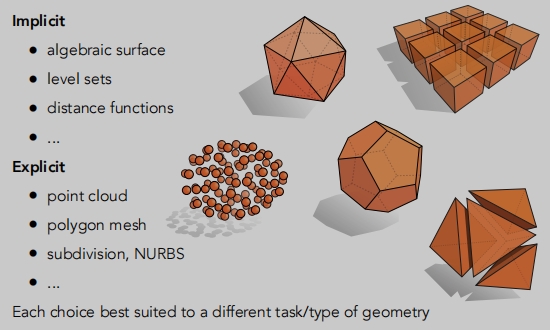
什么是隐式几何：

• 代数曲面
• 水平集
• 距离函数

什么是显示几何：

• 点云
• 多边形网格
• ...

隐式几何 ​

点满足某些特定的关系

三维图形中的所有点，其中x²+y²+z² = 1，满足 f(x，y，z)= 0

红色表示1

蓝色表示-1

f=0，我们如果找到所有的f=0的点，它就可以形成一个几何图形，这就是隐式的几何。

隐式几何的表达方式

坏处：

在f（x，y，z）= 0 时，它是什么？其实它是一个圆环。

隐式的几何，它是不直观、很难直接描述几何图形。

好处：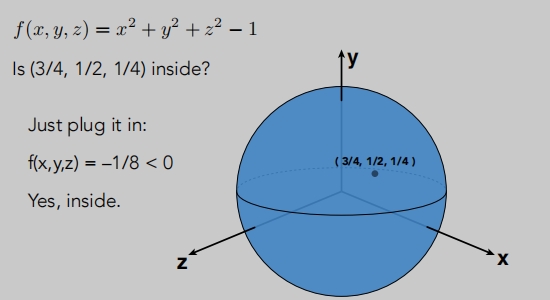

(3/4, 1/2, 1/4) 这点在不在几何内？

隐式几何可以很容易判断出他们的几何关系。

显示几何表示方式方法

• 一种是直接用几何图形表示。
• 还有一种是通过使用函数参数映射方式。

只要把每一个点找一边就能获得几何图形。

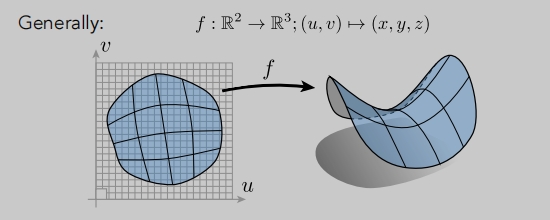
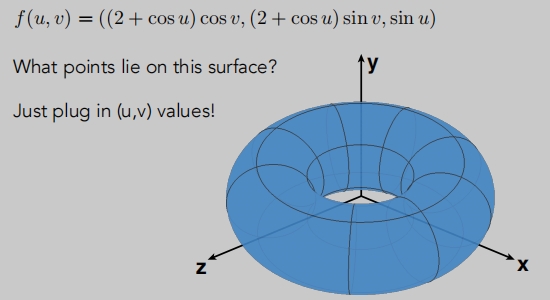
通过u v 参数映射

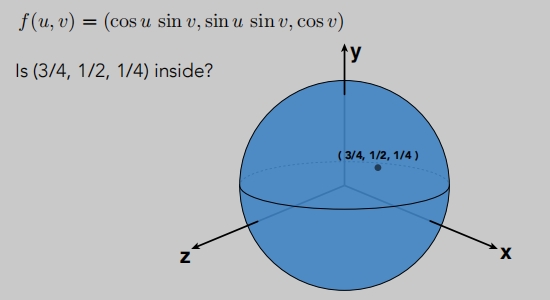
通过u v 参数映射，几何关系没那么容易判断。

没有哪种表示是绝对的好和坏。根据具体情况使用合适的方式。

CSG表示几何（几何隐式表示） ​

通过布尔运算组合隐式几何图形。（有非常广泛的应用）

• 通过基本几何的基本运算，来定义新的几何。

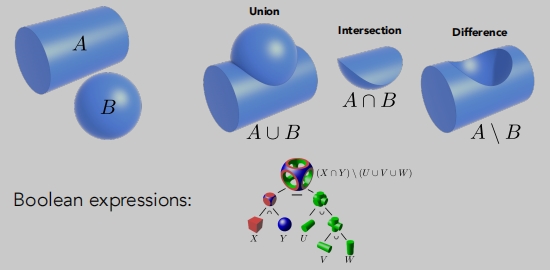
距离函数表示几何（隐式） ​

距离函数：给出从任何地方到对象的最小距离（可以是有符号(正负)的距离）

例如：混合（线性交错线）一个可移动的边界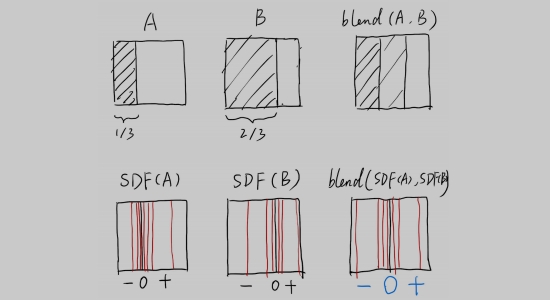

S 表示正负

DF 表示距离函数

可以记录几何边界。

纯距离函数表示的场景

水平集表示几何（隐式） ​

水平集和距离函数其实是一样的，只是表现行式不一样。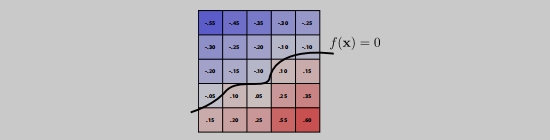

距离函数等于0的位置，它表示的就是物体的表面。

表面的插值等于零提供了更明确的控制形状（如纹理）

水平集在地理的等高线上有广泛应用。

水平集也可以是定义在三维上的格子，这就与前面的纹理联系上了。

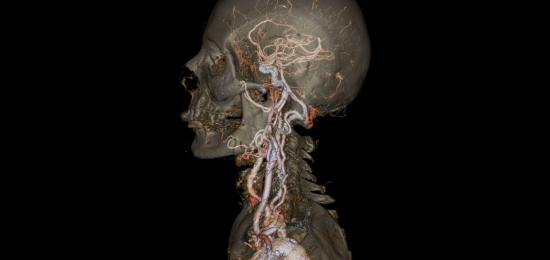
假设我们有一个三维的纹理，表示的是人体各个部位的密度。

如何从这个三维的信息提取出物体的表面呢？

我们可以密度函数等于某个值，然后找到所有满足这个值的位置，这样我们就可以获得这个表面，然后也可以和纹理结合在一起。

水滴效果

也可以通过距离函数(水平集)获得水滴与水面融合后的表面。

分形表示几何（隐式） ​

自相似的意思（类似于计算中递归）

分形在计算图形学中，在渲染的时候会引起强烈的走样，这在渲染中是一个非常大的挑战。

隐式表示的利与弊 ​

优点：

• 隐式函数通常表述起来都很容易(一个公式就可以描述一个形状，这对于存储是非常有利的)。
• 某些查询很容易（内部对象，到曲面的距离），便于处理几个关系。
• 适合射线与表面相交（光线于物体表面）
• 对于简单的形状，精确的描述/无采样误差。
• 易于处理拓扑结构中的变化（例如，流体）。

缺点:

• 很难模拟复杂的形状。