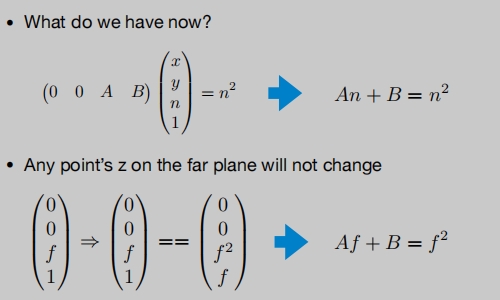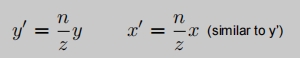三维图形变换 ​

三维空间变换 ​

矩阵表示：

缩放变换、平移变换矩阵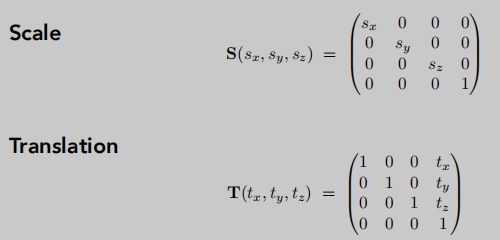

旋转变换矩阵（三维空间中最复杂的变换）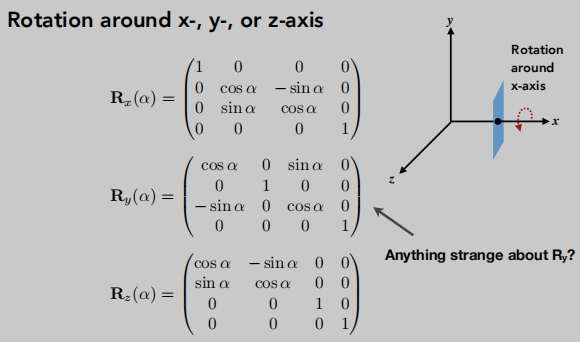

任意角的旋转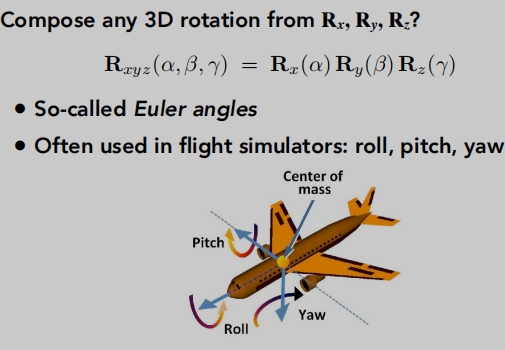

罗德里格斯的旋转公式

旋转轴默认过远点 对任意旋转变换，给出一个旋转矩阵。

当我们想要围绕某一个点旋转

先将这个移到原点。

在进行旋转。

在将所有的变换恢复到原来的点。

罗德里格斯的旋转公式推导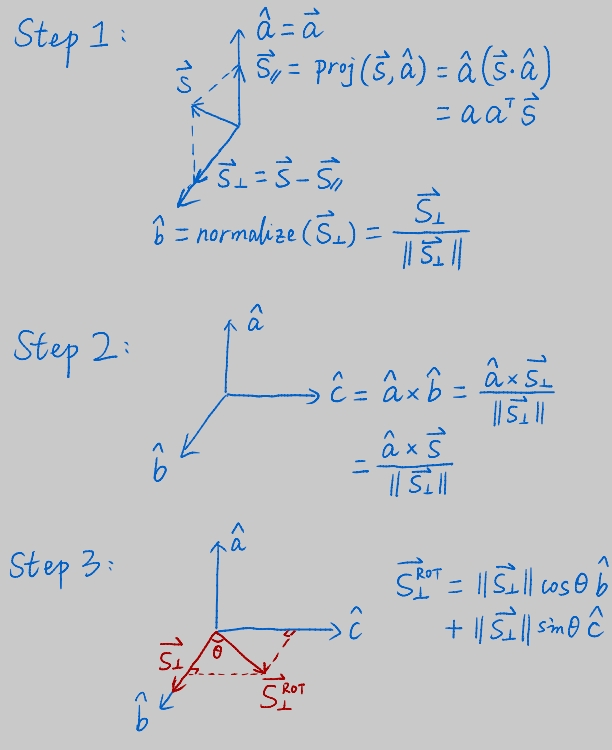

四元数 用于旋转与旋转的差值计算。（旋转矩阵不适合做差值计算）

三维变换 ​

• 视图变换
• 投影变换
  • 正交投影
  • 透视投影

什么是视图变换？

视图变换/相机 ​

定义相机

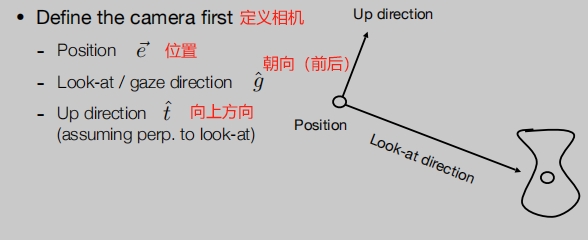
约定相机的初始位置

• 原点：（0，0，0）
• 朝向：-Z
• 向上方向：Y

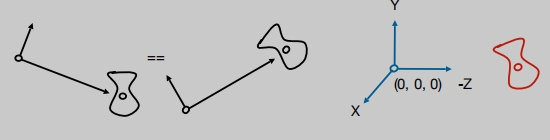
如何初始化相机的初始位置？ 一 一对应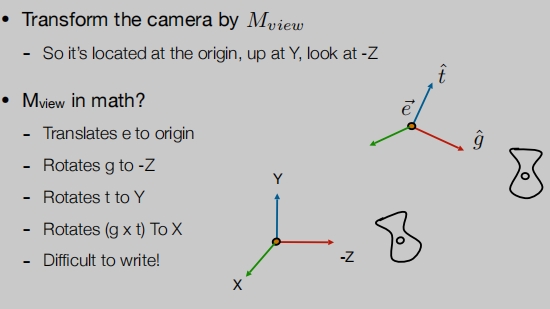

相机初始化写成矩阵的行式（先平移再旋转）

视图变换：相机为了设置为一个约定位置，其他所有的物体也要跟着变换，保证相机与物体保持不变。

视图变换操作的是相机，物体模型要跟着变换，做相对运动。

模型变换与视图变换经常在一起，被称为模型视图变换。

投影变换 ​

• 3D 到 2D
• 正交投影
• 透视投影

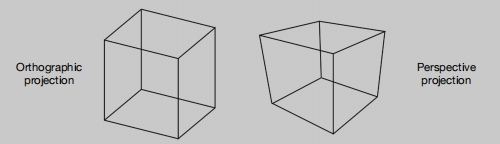
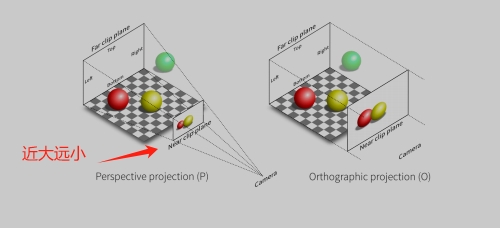
正交投影 ​

一种简单的做法是:

相机位于原点，看着-Z，Y向上。

Z 降维。

变换生成的矩形扩展为二维矩阵。

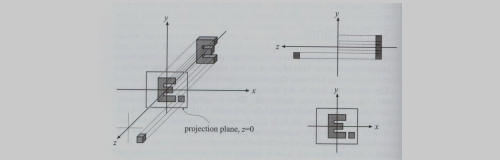
还有一种标准的做法是：

把一个长方体映射到“典型的（正则、规范、标准）”立方体。

通过转换中心长方体。

通过转换中心长方体。

先平移（中心到原点），后缩放（长度/宽度/高度到2）

为什么是2，因为是从中心原点向正负坐标各延申1个单位长度。

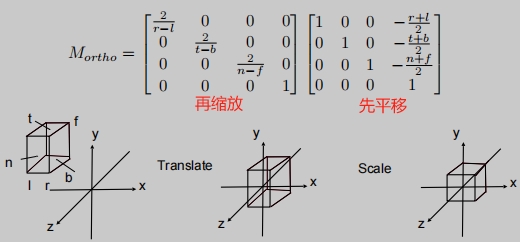
因为我们是沿着-Z方向看，所以 n > f。

这与左/右定则有关。

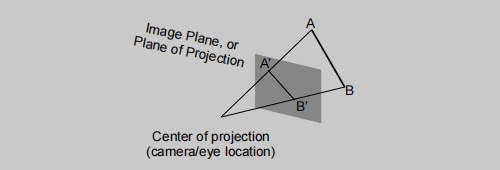
透视投影 ​

• 最常见的是计算机图形学，艺术，视觉系统。
• 满足近大远小。
• 平行的直线将不再平行，收敛于单点。

回顾齐次坐标：

（x、y、z、1）、（kx、ky、kz、k != 0）、（xz、yz、z²、z != 0）在3D中都表示同一点（x、y、z）

透视投影分为两步：

1. 先像远平面挤压到近平面。
2. 再进行正交投影。

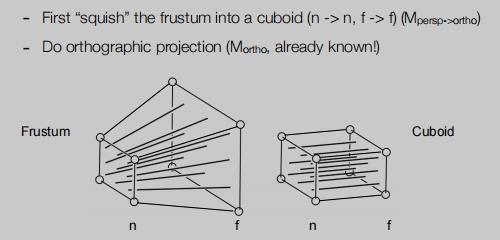
挤压步骤：

近平面不变。

远平面Z 值不变，只是向近平面收缩。

远平面的中心点不变。

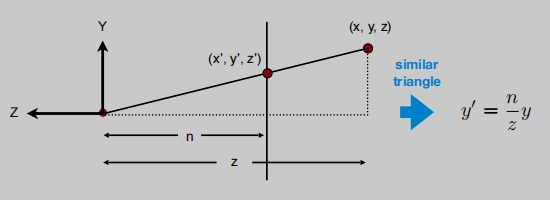
这描述的是Y，X是同样的道理。

挤压用齐次坐标表示：

求变换矩阵：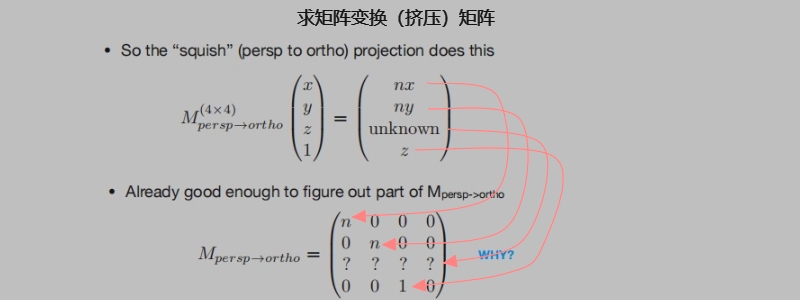

变换矩阵的第三如何求呢？观察挤压步骤发现：

①、近平面上的任何一个点都不会改变。

②、远平面上的任何一个点的z都不会改变。

③、远平面的中心点不变。

根据上面①、② 可以得到变换矩阵的第三行前面两个：（0 0 A B）

再根据 ③ 可以求出A 和 B