线性代数
涉及的学科有:
- 基础数学:线性代数、统计学、微积分;
- 物理:光学、力学、波动光学;
- 信号:信号处理、数值分析;
- 美学;
更依赖于线性代数
- 向量(点积、叉积等)
- 矩阵(矩阵-矩阵、矩阵-向量多重等)
点是向量 (?), 平移或旋转对象等操作,可以是矩阵向量乘法
向量
单位向量
向量的加法
几何上:可以使用平行四边形法则或者三角形法则。 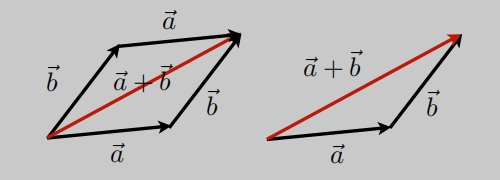
模长: 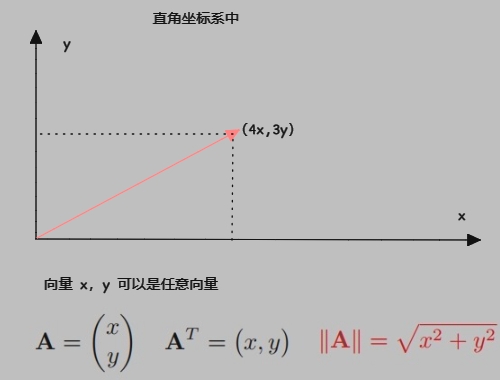
点乘
点乘的结果是一个数。 
向量点乘可以快速算出两个向量的
夹角余弦、夹角。
点乘的运算性质:满足交换律、结合律、分配律。 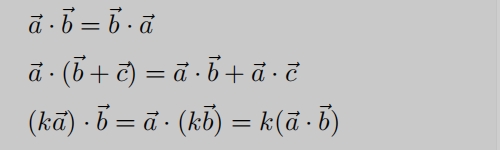
具体运算: 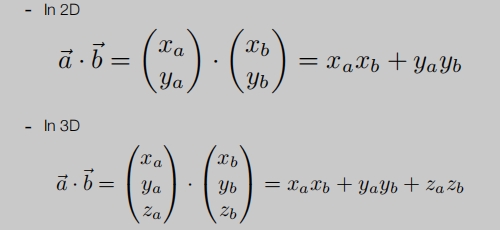
点乘在图形学中的作用
- 找到两个方向(向量)之间的夹角。
如:在光照模型中,光源照的方向,光照法线,反射,摄像机视角等它们之间的夹角。
- 一个向量投
影到里一个向量上。 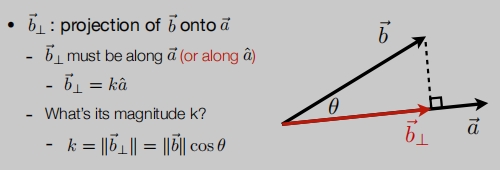
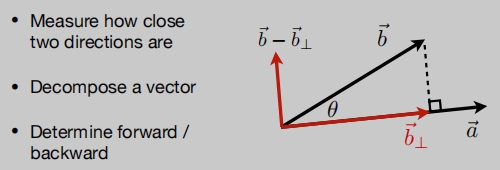
计算投影距离。
分解向量。
在图形学中,点乘还可以计算两个向量有多么接近(根据点乘结果)。
通过点乘可以知道
前与后的信息。 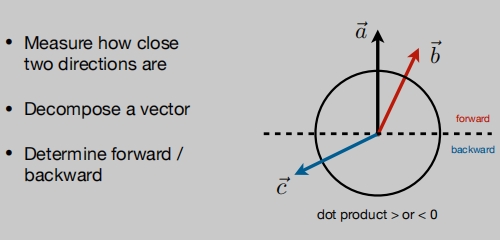
叉乘
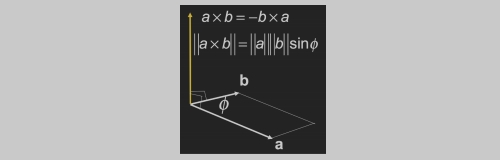
- 叉乘可以得到一个新的向量,该向量垂直于做叉乘的两个向量。
- 这个新向量的方向,由
右手(螺旋)定则决定。(该文档以右手定则为例) - 可用于建立三维直角坐标系。
叉乘的运算性质: 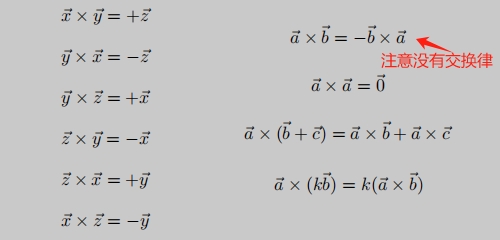
具体运算: 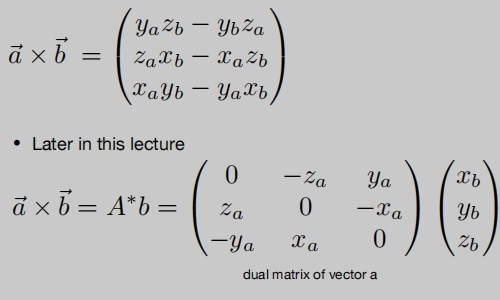
叉乘在图形学中的作用
- 判定左右(顺时针、逆时针)
- 判定内外(都为左或者都为右)
向量叉乘,得到的一个新向量,利用它的正负去判定。(做光栅化的基础)
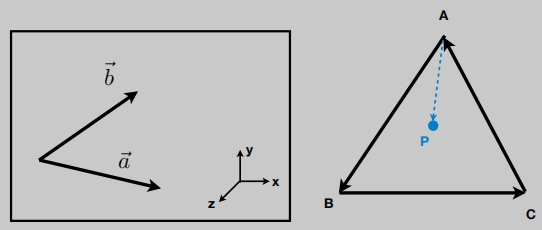
定义一个右手定则的三维坐标: 
矩阵
矩阵与矩阵相乘 
矩阵与矩阵相乘的运算性质 
矩阵应用:如何将一个向量变换为它的y轴镜像 