纹理映射
纹理:是物体表面的特征信息。
它可以是任何类型的图像、图案或模式,可以是静态的也可以是动态的,用来添加细节和丰富物体的外观。
材质:是物体本身的物理信息。
如:颜色、光泽度、透明度、反射率和折射率...
着色:对不同的物体应用不同的材质的这么一个过程。
着色器程序
- 程序顶点和片元处理阶段。
- 描述在单个顶点(或碎片)上的操作。

着色器函数对每个片段执行一次。
输出在当前碎片的屏幕样本位置的表面颜色。
此着色器执行纹理查找以获取此时曲面的材质颜色,然后执行漫反射照明计算。
着色器是一门值敬畏的语言,可以做出非常震撼的效果。
纹理映射(纹理贴图)
在三维空间中,每个三维曲面点在2D图像(纹理)中也有一个位置。 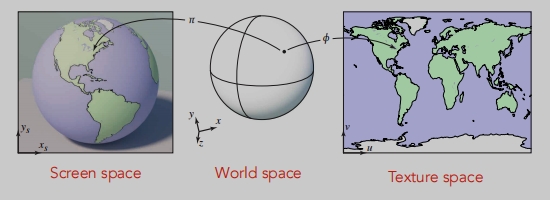
应用于曲面的纹理: 
三维中的三角面,纹理中有对应的图形。
UV坐标
每个三角形顶点指定一个纹理坐标(u、v) 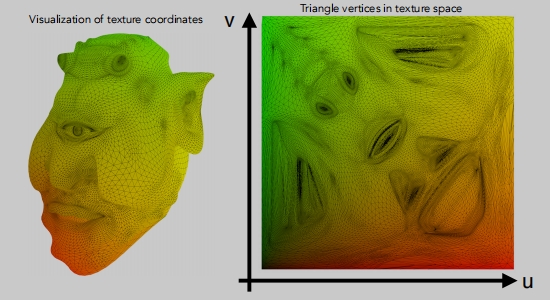
绿色:v方向
红色:u方向
UV坐标的可视化

好的纹理设计能无缝衔接。 
如果知道三角面的三个顶点的uv坐标,如何知道三角形内部每个像素的uv 坐标?
可以通过插值的方式获得(利用重心坐标)
重心坐标
如何在三角形内部任意插值?为什么要在三角形内部插值?
当我们知定顶点处的值,我们希望获得三角形内部的值。
并且在三角形内部获得平滑过渡的值。
可以插值什么内容?
纹理坐标,颜色,法向量 ……。
怎么做呢?
利用重心坐标。
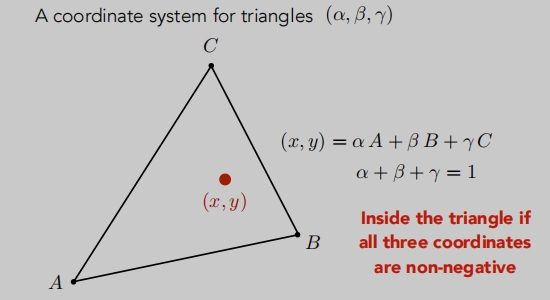
- 重心坐标是定义在一个三角形内部的。
- 在三角内任意点与三个顶点的关系都可以表示成为一个线性组合:(x,y)= α A + β B + γ C
- 满足 α + β + γ = 1 ,α,β,γ 是三个非负数。当知道其中两个数后,就能得到第三个数。
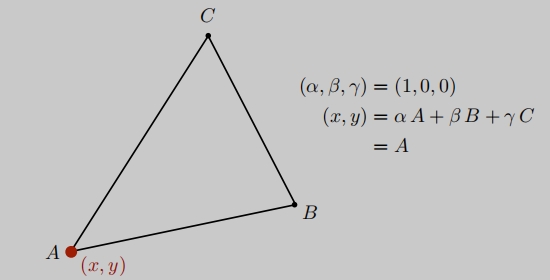 A点可以写成:
A点可以写成:
(α, β, γ) = (1, 0, 0)
(x, y) = α A + β B + γ C = A
重心坐标也可以通过面积比求出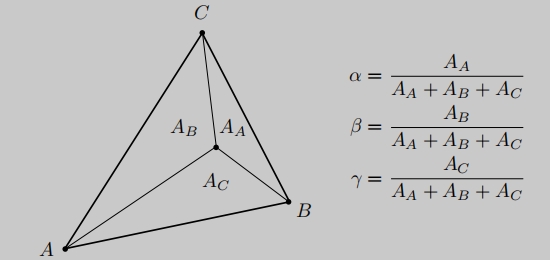
三角形的重心点(通过面积求坐标) 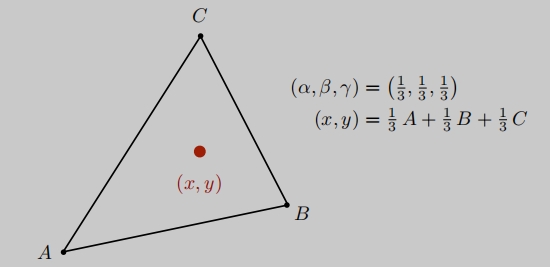
重心坐标计算公式:
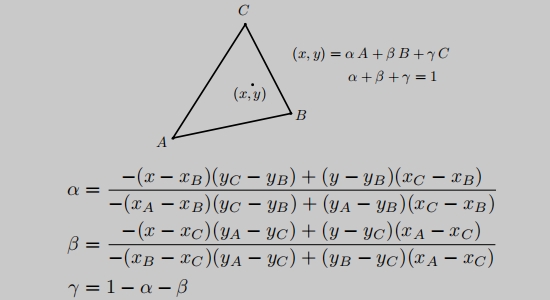
应用重心坐标做插值:
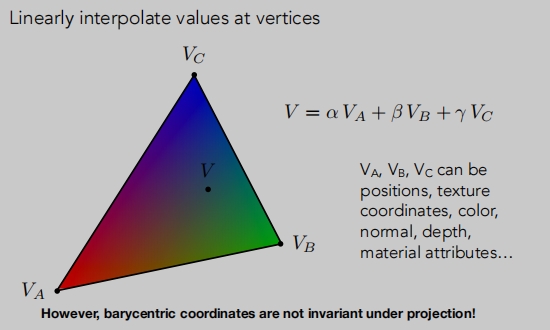
重心坐标插值可以是:位置、纹理坐标、颜色、法线、深度、材质属性...
注意
重心坐标,在投影下会得到不一样的重心坐标。
如果我们想要插值三维空间中的属性,我们就应该取三维空间的中的顶点坐标,进行重心坐标计算和插值,而不等投影完成后。
纹理映射过程

- 对于任意一个点(x,y),可以使用
重心坐标计算出它的uv坐标。 - 在纹理上查询uv坐标的值:
texcolor = texture.sample(u,v) - 然后对该点的值进行处理。
纹理太小
纹理上的像素:纹素 / 纹理元素(texel)
如果纹理太小怎么办?(高像素的物体,低像素的纹理)
纹理太小了,就会被拉大。
物体上每一个像素点我们都可以找到它对应的在纹理上的位置,但是在纹理上它可能不是整数,我们会把他四舍五入成为整数(0.4 = 0,0.6=1),在一定范围里,我们认为查找的是相同的纹理像素。 当纹理太小时,一定范围里的 pixel(3 * 3 或者 5 * 5) 会映射 同一个 texel。此时就会产生锯齿。
如何解决这一问题?
当我们在查询纹理坐标的时候,如果获取到的是非整数坐标,我们要求取它的值,使得纹理更平滑。---- 使用双线线插值。
双线性插值
线性插值:
lerp(x, v0, v1) = v0 + x(v1 − v0) (求 x 往哪个值靠近)
假设v0, v1分别是0,1,x 就是0-1之间的值。
当x = 0 的时候,x = v0;当x = 1 的时候,x = v1。
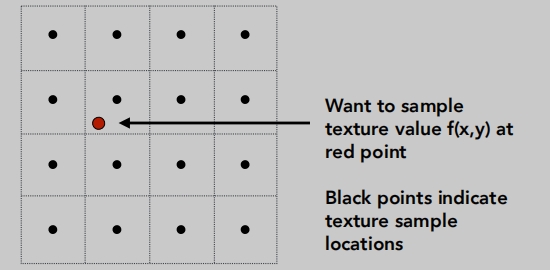
双线性插值
在水平方向和垂直方向做线性插值。 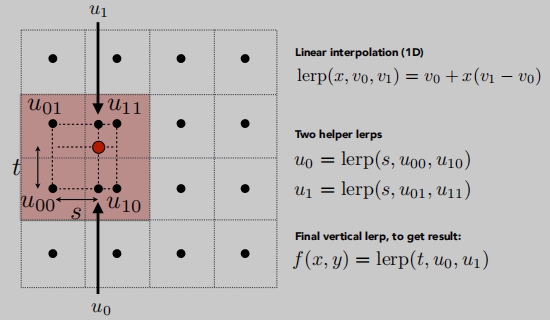
此时得到的纹理颜色就是周围四个点颜色的平均。

Nearest 四舍五入的方式
Bilinear 双线插值的效果
Bicubic 双线三次 (取周围16个点,运算量大,但精细)
纹理太大
 出现了 什么问题呢?
出现了 什么问题呢?
远处摩尔纹
近处锯齿(走样)
怎么产生的呢? 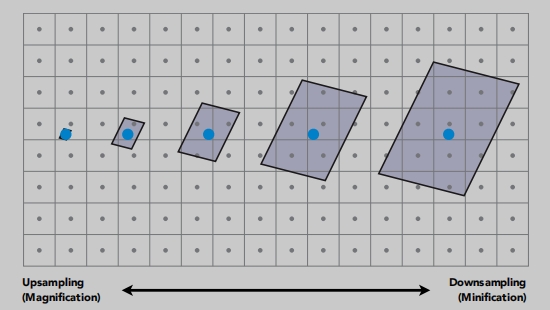
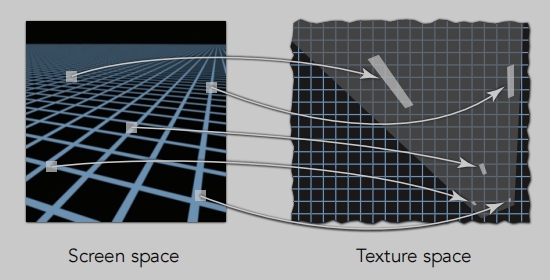
屏幕中,每个像素对应的纹理大小是各不相同的。
有的一个
像素占用了很大一块纹素(如:1个像素点,在9个纹素点采样)一个像素在一个很大区域的纹素中取平均,这个平均无法代表这个区域的纹素的。这会导致与上一个像素采样的不连续。
总结:像素 与 纹素 采样频率无法很好的匹配。(有的需要高频,有的需要低频)
超采样会的效果怎样呢?
- 质量高,但是昂贵。
让我们用另一种方式来理解这个问题:
- 如果我们不采样会怎样?
- 如果我们能立刻知道一个范围内的平均值即可。
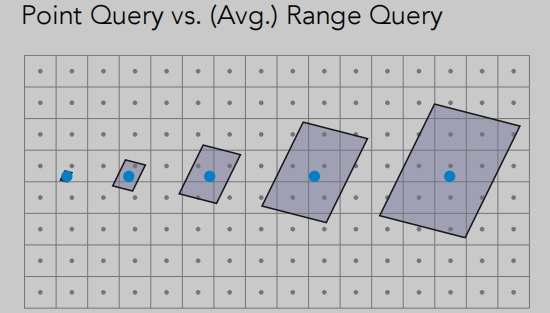
这里就牵涉到 点查询、范围查询的问题。
图形学中用
Mipmap来解决范围查询这一问题。
 假设应用的是相同的纹理:
假设应用的是相同的纹理:
近处的像素对应的纹素范围就小。
远处的像素对应的纹素范围就大。
Mipmap
Mipmap的特点:
- fast:图形学中用
Mipmap来解决范围查询,非常的快。 - approx:近似(不是正确的)
- square:方形。
Mipmap只能做近似的、方形的、快速的范围查询。

把一个纹理图片分成了多份。
图像金字塔 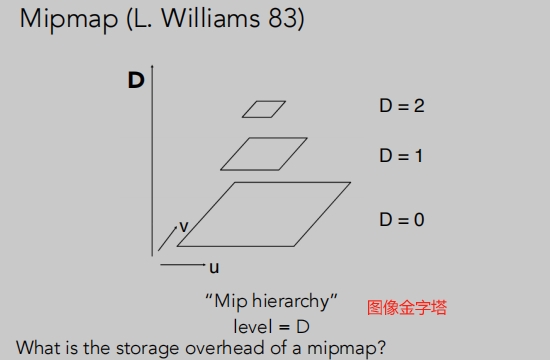
Mipmap新增的存储开销比原来多了
三分之一。
我们要用Mipmap做一个近似的在正方形区域内做范围查询,且立刻要得到区域内的平均值是多少。
任何一个像素都可以映射到一个纹理区域,这个区域我们要如何得到呢?我们可以用
近似方法得到。
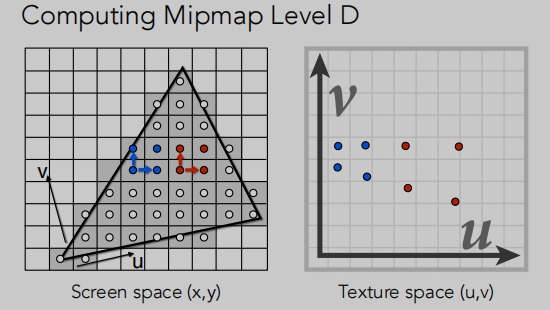
使用相邻像素样本的纹理坐标来估算纹理大小。(这里其实就是在一个“近似”)
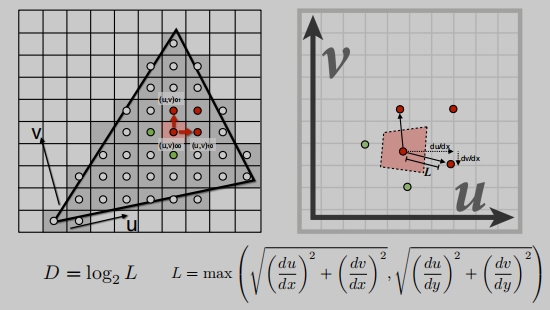
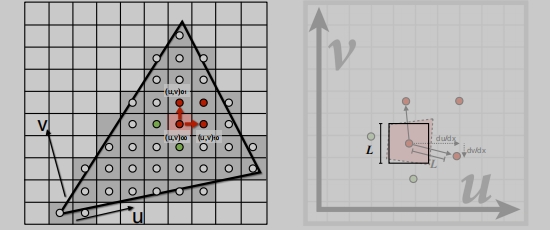 这里非常有意思:
这里非常有意思:
上面的做的“近似”,其实就是在计算,一个像素,在纹理中所占纹素大小。
1个像素在屏幕中相当于是最小单位,“近似”做的事情就是将,
单位像素类比为单位纹理----个人理解。
在做完“近似”之后的正方形,我们如何根据我们之前预计算好的Mipmap进行查询这个正方形纹素区域的平均值呢?
假设这个区域的大小是1像素,对应1*1个纹素,此时我们需要去
原始的纹理图层(D0)中去找到这个对应的位置(一一对应)。假设这个区域的大小是1像素,对应4*4的纹素,此时我们需要去
第三层纹理图层(D2)中去找到这个对应的位置(一一对应)。具体层级 D = log2 L 。
不连续性问题: 
不连续性是应为Mipmap 只存在整数层,不存在小数层。
我们无法知道0.5层,0.8层对应的 Mipmap图层的值是什么?
三线性插值解决这个问题。
三线性插值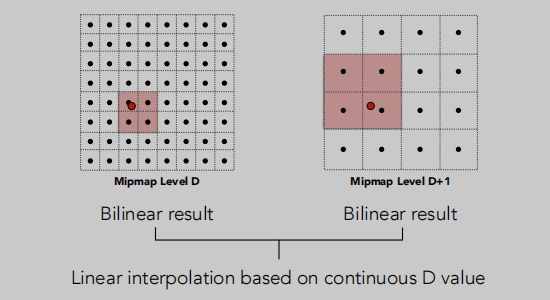
它可以得到非常平滑的值
首先它是做了相邻层级的区域查询,将其查询结果分别进行双线性插值
把相邻层级的两个双线插值结果合在一起。
然后再层与层之间再做插值。(在双线插值的基础上加了一层线性插值 = 三线性插值)
此时同过相同计算,我们就可以在任意层(管他是整数层,还是浮点数层)去查询它的值。
三线性插值的效果
三线性插值的开销:并不大。
做两次查询。
一次插值。
各向异性过滤
Mipmap trilinear sampling 真的完美了吗? 
Mipmap三线性插值: 远处的像素糊掉了。
各向异性过滤: 效果会好一些(各向异性过滤可以解决部分问题,任然存在一些问题)。
各向异性:在不同方向上,它的表现各不相同。(水平和垂直方向上的表现完全不相同)
- 在水平和垂直方向上进行压缩。

从水平方向看,高度不变。
从垂直方向看,宽度不变。
Mipmap只是各向异性过滤对角线上的压缩,各向异性过滤比Mipmap多了是不均的水平方向和垂直方向的压缩。将压缩的图片恢复到原来的图片,通过做这样的预计算,我们可以非常快查询到原始对应的图片被压缩后的矩形区域,而不是限制在Mipmap的正方形。
各向异性过滤对于矩阵区域可以快速的范围查询(比Mipmap好),不用限制在正方形区域,对于非矩阵的也没能解决。
各向异性过滤开销:是原来的三倍。
只要显存足够,各向异性过滤对应用的性能几乎没有什么影响。
EWA过滤: 
效果好,代价是开销大。
纹理应用
在现代gpu中,纹理=内存+范围查询(过滤),不要把它局限于图片,可以把它理解成数据。
 环境贴图
环境贴图
来自环境的光线与环境一起渲染。
 环境照明
环境照明
环境贴图(左),用于渲染真实的照明。
可以把球面环境图记录下来,并且可以展开。
Spherical Map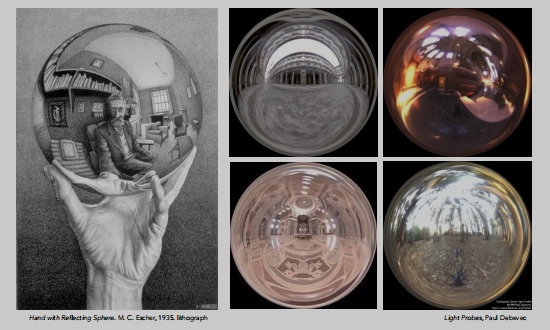

容易变形(顶部和底部部分)被极度压缩。
这里就有了
Cube Map来解决 被压缩这一问题。
Cube Map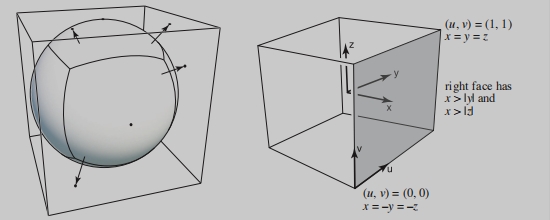

法线贴图(凹凸贴图)
人为的在任意点做一些虚拟的法线出来,通过纹理映射,得到凹凸不平的效果,物体几何本身是没有任何变化的。 
假设左上的贴图:黑色部分为0,白色部分为1。
根据这些信息我们可以在这些位置重新构造出虚拟的法线,通过纹理映射得到凹凸不平的阴暗效果。
法线贴图具体做了什么事情? 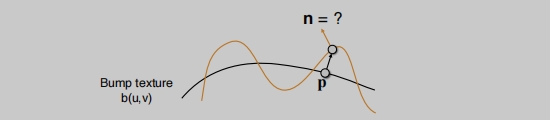 通过
通过法线贴图添加曲面细节,而不添加更多的三角形,不会对原本的几何做改动。
把任一像素的法线做一个绕动,通过定义临近位置的高度差,来重新计算它的法线。
应用
法线贴图它会告诉我们高度位置会如何变化。(p的位置被向上移,法线指向n)
二维示例中:法线贴图如何计算法线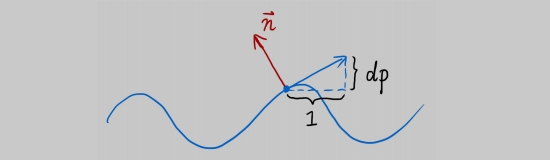
假设原本是平面P点,蓝色的曲线是
法线贴图定义出来的。原本的法线为(0,1)p点的
切线计算为:p处的导数 dp = c * [h(p+1)- h (p)]它的法线垂直于切线,把切线逆时针旋转90度就能得到它的法线。
三维中法线贴图
- 原始表面法线n (p) = (0,0,1)
- uv方向的切线:
- dp/du = c1 * [h(u+1) - h(u)]
- dp/dv = c2 * [h(v+1) - h(v)]
- 法线为 (-dp/du, -dp/dv, 1).normalized()
- 请注意,这是在本地坐标中进行的!
位移贴图
位移贴图是 法线贴图(凹凸贴图)一种更高级的做法。
- 位移贴图实际上是真是的改变了各个顶点的位置信息。
- 位移贴图对模型的三角面足够细致。

可以从贴图边缘,和物体投影看出差异。
如果一个物体模型三角面没有那么细致,能使用位移贴图吗? DirectX(windows)提供了动态曲面细分方法。
三维噪声函数
纹理可以是三维的 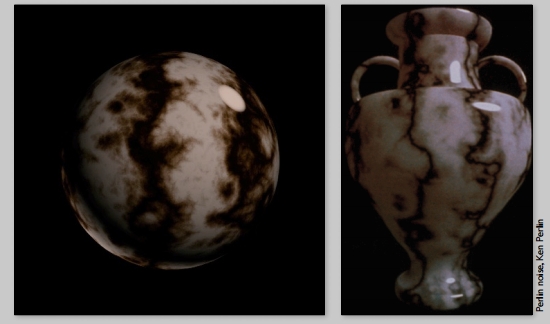
这里并没有二维纹理图像,而是定义了一个三维空间的噪声函数。
三维噪声函数还可以应用在山脉的起伏高度。
预先计算纹理
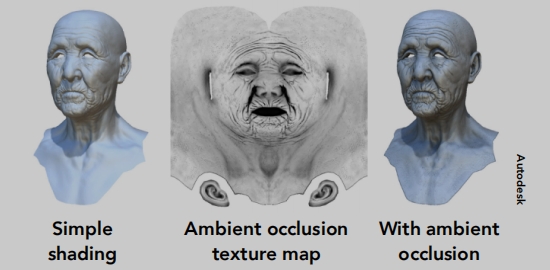
把很多计算提前去做,做完了再去应用它,就会非常快了。
就是利用纹理去记录一些提前计算好的信息。
三维纹理和体积渲染
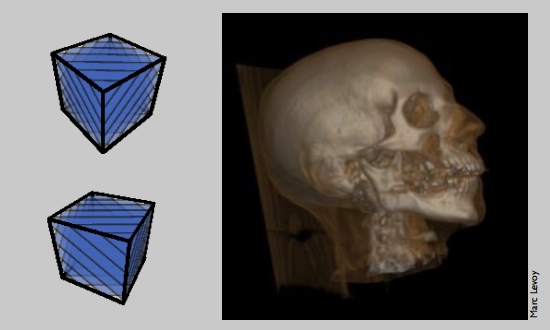
如:通过核磁共振扫描得到一些三维的信息(组织的密度...),然后渲染出这些信息。