变换
什么是变换
三维成像(三维投影到二维) 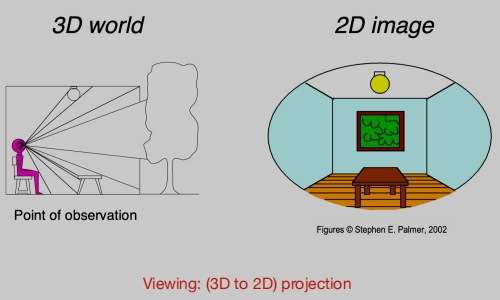
变换的应用:
- 投影成像
- 动画
二维变换
将矩阵与变换关联起来。
Scale(缩放变换)
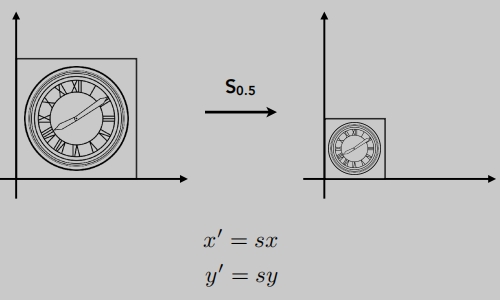
缩放矩阵: 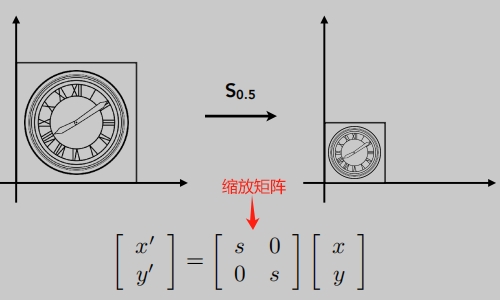
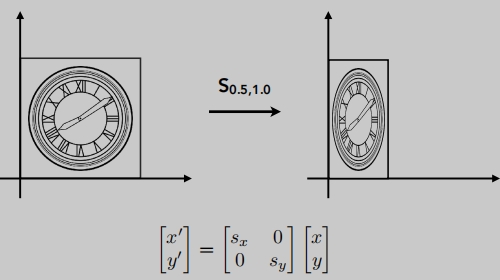
反射矩阵(镜像) 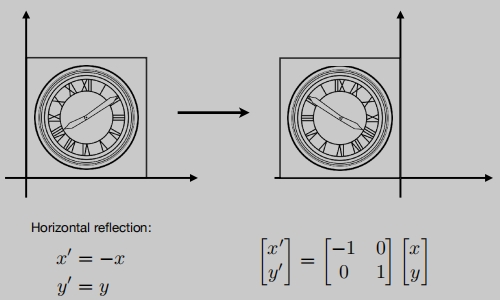
切变矩阵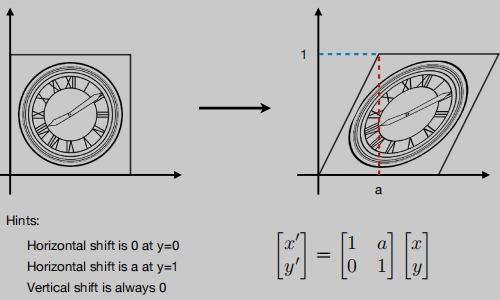
Rotate(旋转变换)
默认是绕着原点旋转(0,0),逆时针方向。 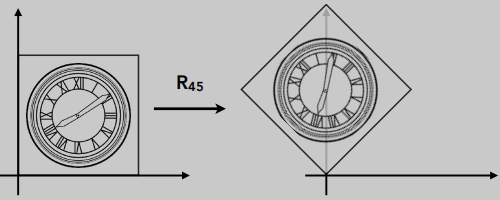
旋转矩阵(必需自己能推导) 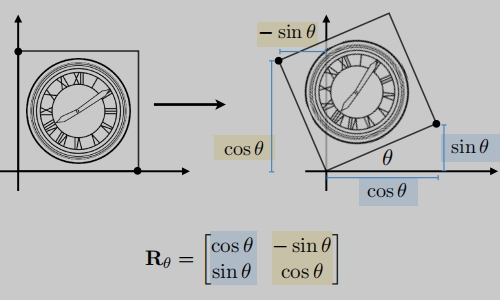
注意旋转角度的正负
线性变换
- 他们的共同点:可以通过线性变换得到变换后的坐标。(将
变换与矩阵关联起来)。 - 对于变换就用矩阵来表示:
矩阵乘以向量的行式。
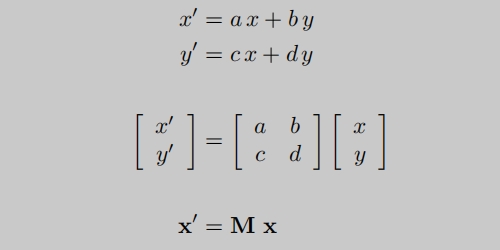
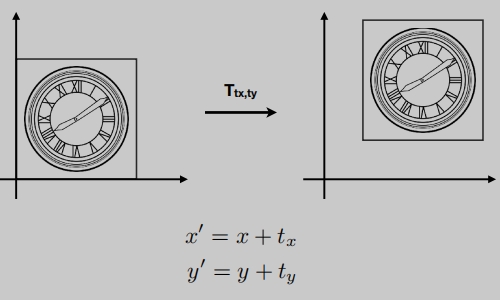
Translate(平移变换)
写成矩阵的行式: 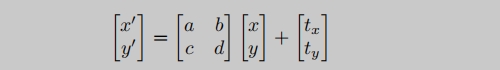
平移变换无法直接使用矩阵乘以向量的行式来表达。- 然而我们也不希望
平移变换成为特例。 - 是否存在一种统一方式来表达所有变换---> 解决方案:
齐次坐标。
齐次坐标
- 添加一个维度的坐标轴。
齐次坐标下的平移变换以矩阵乘以向量的行式: 
齐次坐标下所有的变换操作依然是有效的 
仿射变换
线性变换(缩放、旋转)+ 平移变换 统称为 仿射变换。 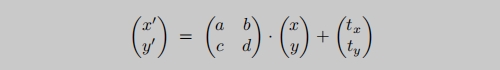
仿射变换的矩阵乘以向量行式: 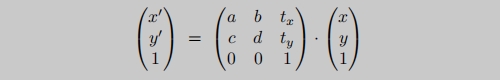
仿射变换矩阵
逆变换
在线性变化中等于乘以它变换矩阵的 逆矩阵
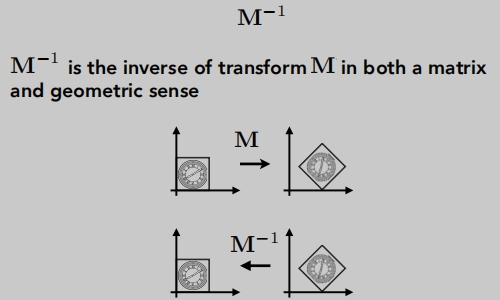
组合变换
先旋转还是先平移?结果是不一样的。 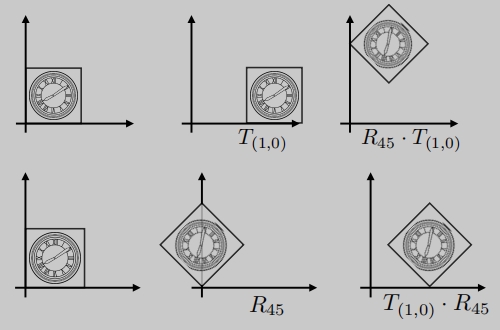
这与
矩阵的不满足交换律的概念是一致的。
组合变换矩阵的运算顺序
给向量添加变换时,一般是左乘一个变换矩阵,总体的运算顺序是从右到左。 
组合变换的推广
预乘n个矩阵,得到一个表示组合变换的单一矩阵 
分解变换
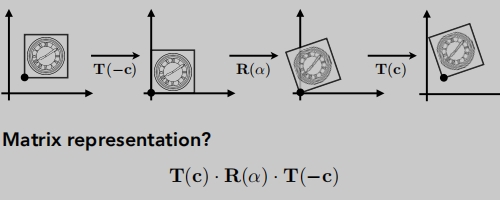
三维变换

齐次坐标三维变换``矩阵乘以向量表示 
视图、投影(正交、透视)变换,总称为观测变换。