几何的面

曲面

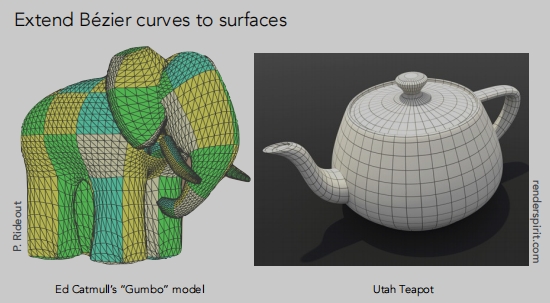
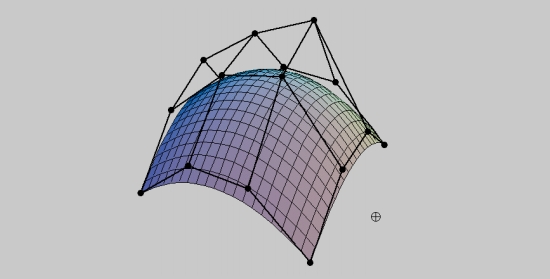
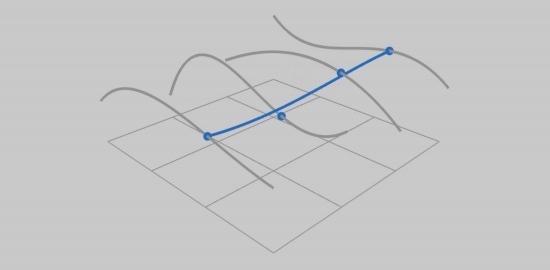
在u 和 v 上（或者说t1,t2）都有对应一个时间 t的贝塞尔曲线。

网格操作

网格细分
网格简化
网格正则化（正则化）

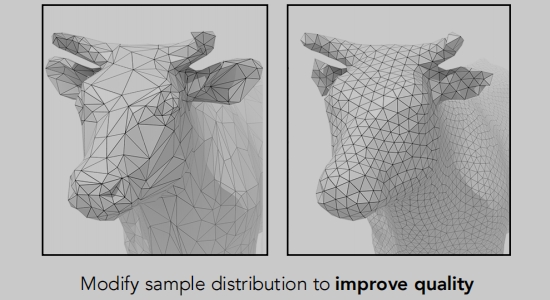
三角面处理成为更近似于正三角形。

三角面细分

引入更多的三角形（增加数量）。
让这些三角形的位置发生一些变化，使得原来的物体变化更平滑。（调整位置）

这里讲的是Loop细分（Loop是一个地面，算法作者所在的地方）

Loop 细分

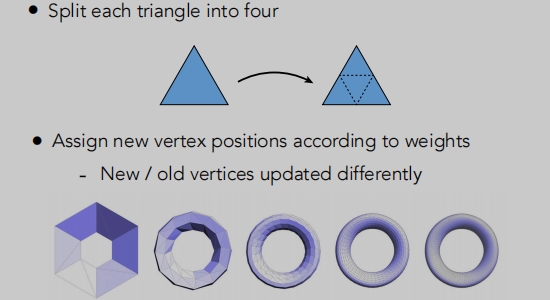
如何增加三角面？连接三角形三条边上的一个点（根据算法获得），从而获得4个小的三角形。
如何调整三角形的位置（调整三角形顶点位置）？根据不同算法配新/旧顶点位置。

新顶点位置调整：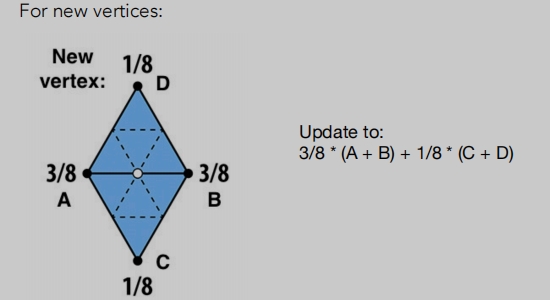

两个相邻共边的三角形ABCD。
根据ABCD四个顶点的位置，利用一种加权平均获得新顶点的位置：3/8 * (A + B) + 1/8 * (C + D)。

旧顶点位置调整: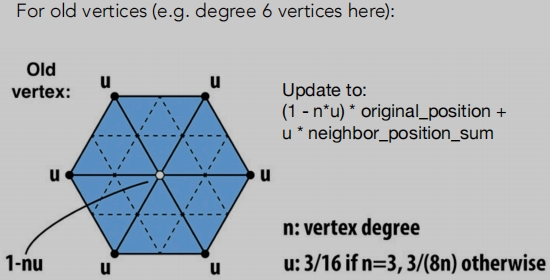

定义一个n，为白点（原点）的所对应的度。
定义一个u，是与n的度对应的一个系数。
根据（1-n * u） * 当前原点位置 + u * 周围加权平均顶点的位置。
这个算法，周围点越多当前点的权重越低，周围点越少，当前点权重越高。

Loop细分示例：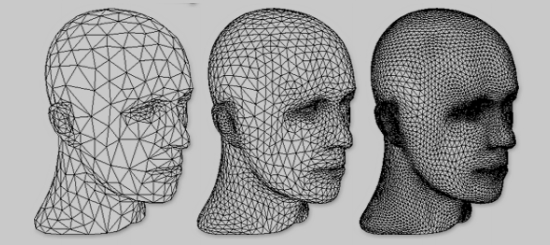

卡特莫尔-克拉克细分（一般网格）

对于三角形网格我们使用Loop细分，对于一般网格（既有三角形也有四边形）我们可以使用卡特莫尔-克拉克细分。

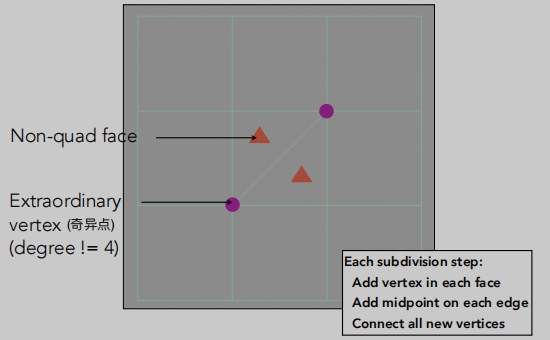
定义四边形、非四边形。
定义奇异点：度不为4的点（degree != 4）。

定义完之后如何进行细分呢（增加网格）？

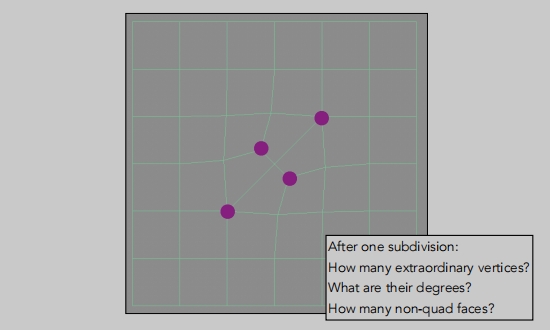
在每个面上添加顶点（面的中点/重心）。
在每个边上添加中点。
连接面和边的中点。
这样我们就增加了网格。

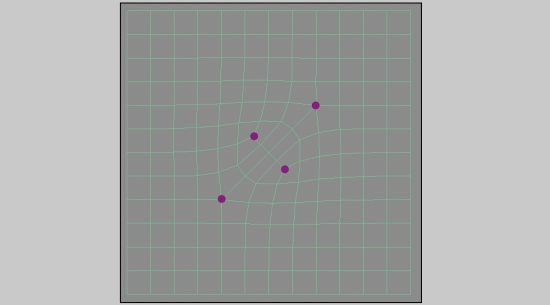
做完第一次卡特莫尔-克拉克细分

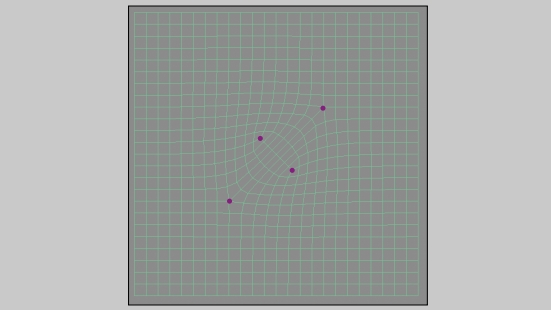
做完第二一次卡特莫尔-克拉克细分

卡特莫尔-克拉克细分的性质：

每一个非四边形面都会引入一个奇异点，并且在引入奇异点之后非四边形面都会消失。

简单来说，在一次卡特莫尔-克拉克细分之后，非四边形面会变成奇异点。

在做完第一次卡特莫尔-克拉克细分之后，会增加非四边形面数的奇异点个数，之后再做细分奇异点个数不再增加。

卡特莫尔-克拉克细分顶点位置调整

计算公式-分为三种类型的点：

f 面中心点
e 共边的中点
v 旧的顶点位置

卡特莫尔-克拉克细分示例：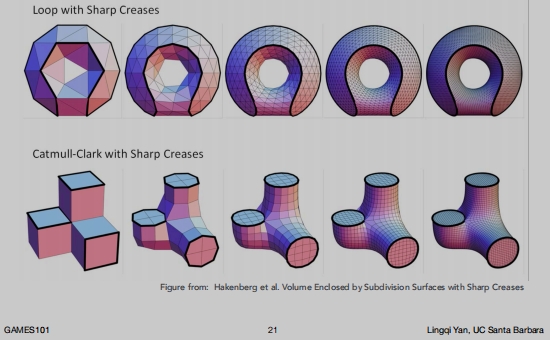

网格简化

边坍缩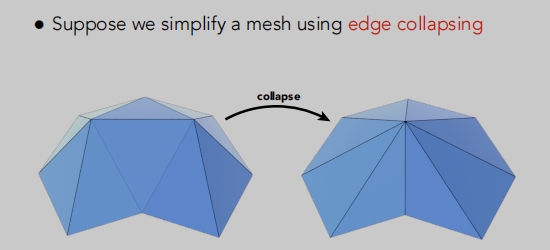

假设我们使用边的折叠来简化一个网格。
边坍缩实现起来并不容易。这里我们使用二次误差度量（二次是平方的意思）实现。

二次误差度量

新顶点应最小化其与先前相关的三角形平面的平方距离之和。

找一个点，使得到达和它相关的面距离的平方和最小。

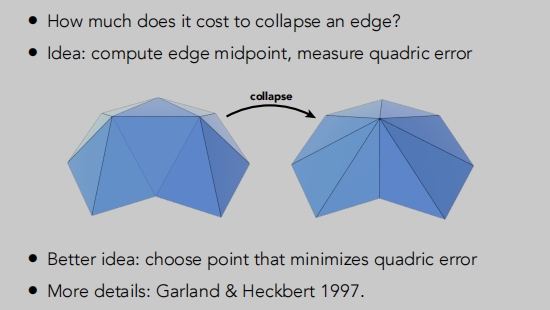
这是一个繁琐复杂的过程，需要解决很多问题。

网格简化深入学习传送门

网格简化示例