几何的曲线 ​

这里主要描述的是显示的几何。前面的说的隐式几很多的表示方法，显示几何同样也有很多表示方法。

三角面

贝塞尔曲面

细分曲面

点云

点云表示几何（显示几何） ​

• 最简单的表示：点列表（x、y、z）。
• 易于表示任何类型的几何图形。
• 适用于大型数据集（>>1点/像素）。
• 经常转换成多边形网格。
• 很难在采样不足的区域中绘制出数据（缺点）。

三角面/多边形表示几何（显示几何） ​

在图形学中应用最为广泛的。

• 存储顶点和多边形（通常是三角形或四形）
• 更易于进行处理/模拟，自适应采样
• 数据结构更复杂
• 是图形中最常见的一种表示

在计算机中三角形面如何形成物体的（.obj格式文件）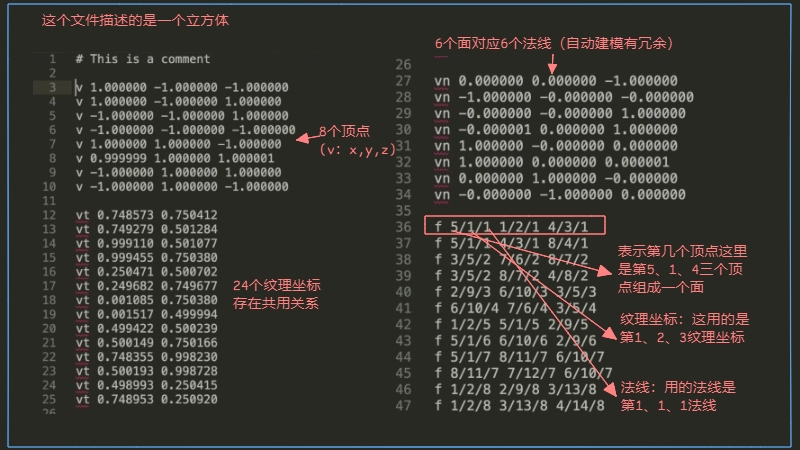

定义好顶点、纹理坐标、法线后然后定义他们之间的连接关系。

贝塞尔曲线表示几何（显示几何） ​

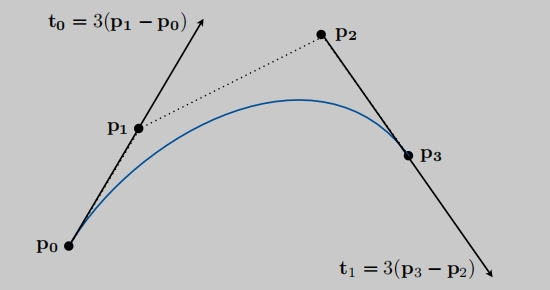
用一系列的控制点去定义曲线。控制点它会定义曲线满足一些性质

一开始沿着P0 到P1 往前走，最终会在P3结束。并且在结束的会沿着P2 到 P3往外走。

如何画出一条贝塞尔曲线？

二次贝塞尔曲线 ​

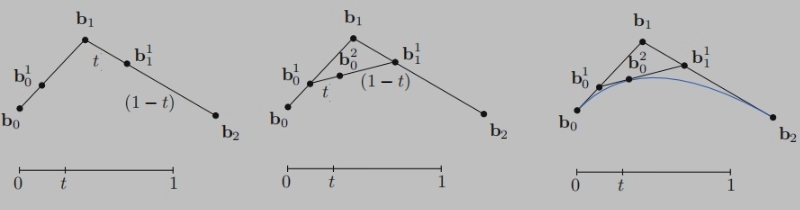根据给出的三个控制点：

我们可以定义它的起点是在时间 0，它的终点是在时间 1，任意时间点为 t。

想要画出它贝塞尔曲线，实则就是要把在它在0-1之间的任意时间 t对应在平面空间中的位置找出来。

简单来说就是：给你一个时间t（在0-1之间），这个点在哪。

①、在b0到b1之间假设 t 位置的长度比为 n，这点记作b10。

②、在b1到b2之间找长度比为 n 的位置，这点记作b11。连接b10和b11得到一个新的线段（两个点）。

③、b10和b11之间找到长度比为 n 的位置，记作b20，此时 b20 就是该贝塞尔曲线上的一个点（一个点）。

根据 t 的不同值（0-1），我们可以求出一个平滑的贝塞尔曲线。

三次贝塞尔曲线 ​

三次贝塞尔曲线也是同样的道理。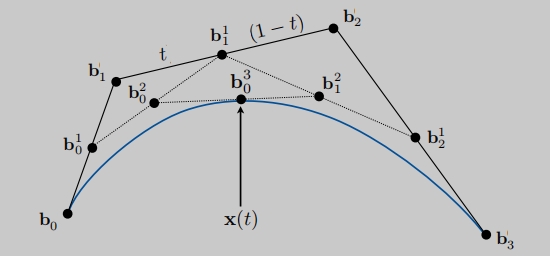

每次减一个点，重复的进行递归。

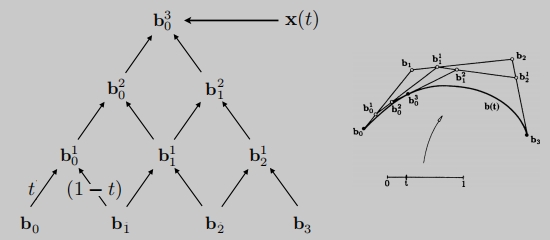
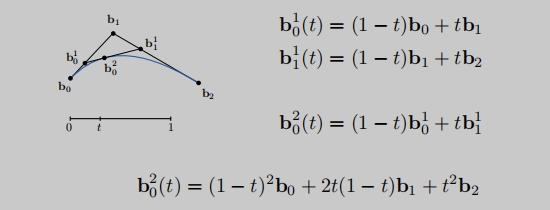
b后面2这里不是平方，指的是第二层。

贝塞尔曲线-代数公式 ​

给定n+1个控制点，我们可以得到n阶的贝塞尔曲线。

这个贝塞尔曲线在任意时间 t 它都是之前给定的控制点的线性组合。

它组合的系数就是一个多项式，这个多项式是与时间有关的。

贝塞尔曲线的任意时间点就是控制点的组合，怎么组合？----用伯恩斯坦多项式进行组合。

坐标可以是三维坐标。

伯恩斯坦多项式 ​

贝塞尔曲线特性 ​

• 贝塞尔曲线必须过起点（t=0）和终点（t=1）。
• 三次贝塞尔曲线系数3 ？
• 仿射变换下：贝塞尔曲线依然一致。（对投影不行）
• 凸包性质

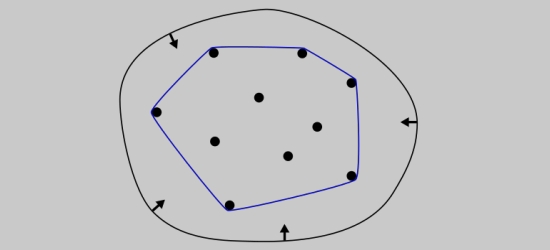
凸包 ​

能够包围一系列给定的几何形体的最小的凸多边形。

逐段贝塞尔曲线 ​

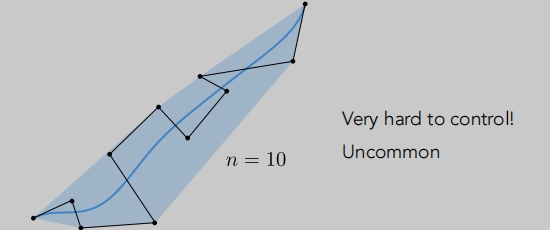
虽然可以绘制出平滑的曲线，但是无法表现控制。

逐段三次贝塞尔是最常见的技术：每四个控制点定义一条贝塞尔曲线。

这里其实有个小问题：连续性问题。

连续性

C0连续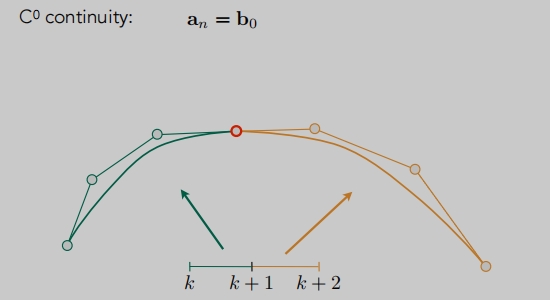

第一段的终点等于第二段的起点（几何上最简单的连续）。

C1连续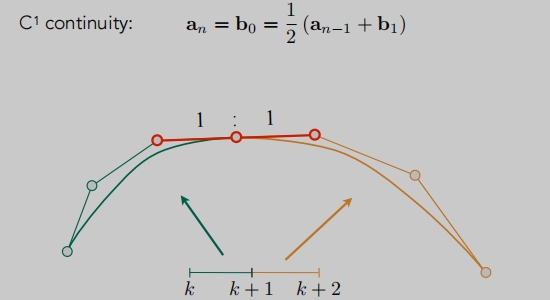

切线也要连续，向临两个控制必须共线，距离相等。一阶导数的连续。

还有要求更高的导数连续...

B-splines（b样条曲线） ​

它是对贝塞尔曲线的拓展。

• 局部性，更可控。（非常复杂）