什么是堆

优先队列（Priority Queue）：它是一种“特殊的队列”，取出元素的顺序是依照元素的优先权（关键字）大小，而不是元素进入的队列的先后顺序。

堆的实现

使用数组、链表表示【堆】的时候，在查找、插入或者删除的时候，总有一些操作复杂度不够小。有没有更好的办法呢？--> 二叉搜索树

二叉搜索树表示【堆】：查找、插入、删除操作复杂度与树的高度相关（O(logn)），问题在于，如果每次都删除、或者插入最大的值，几次操作后，会导致二叉搜索树失去平衡，复杂度就上升了。

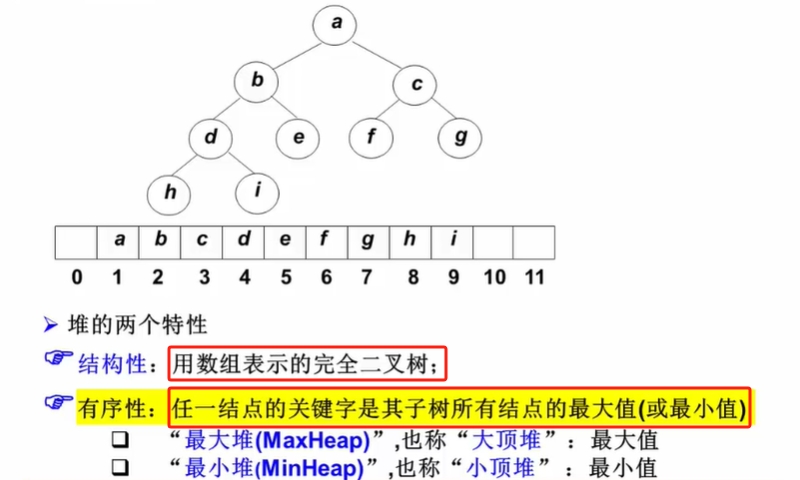
完全二叉树表示【堆】：满足，每个结点的元素值不小（或不大于）于其子结点的元素值。

抽象数据类型描述

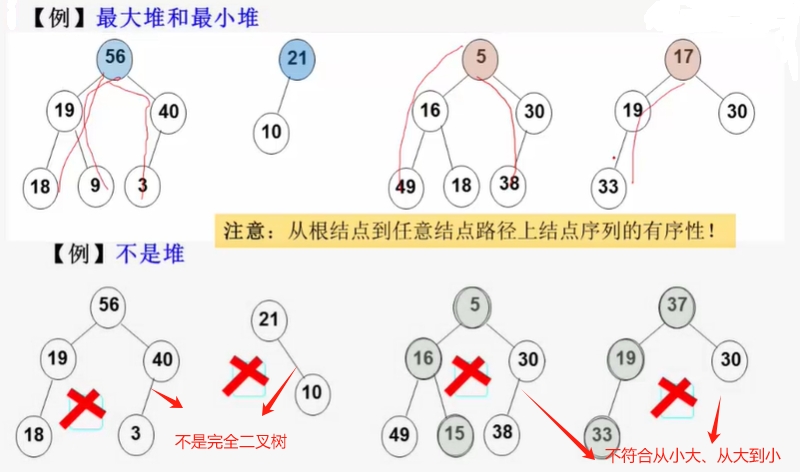
类型名称：最大堆（MaxHeap）

数据对象集：完全二叉树，每个结点的元素值不小于其子结点的元素值。

操作集：最大堆H∈MaxHeap，元素item∈ElementType，主要操作有：

创建一个空的最大堆。
判断最大堆H是否已经满。
将元素item插入最大堆H。
判断最大推H是否为空。
返回H中最大元素（高优先级）。

初始化

插入

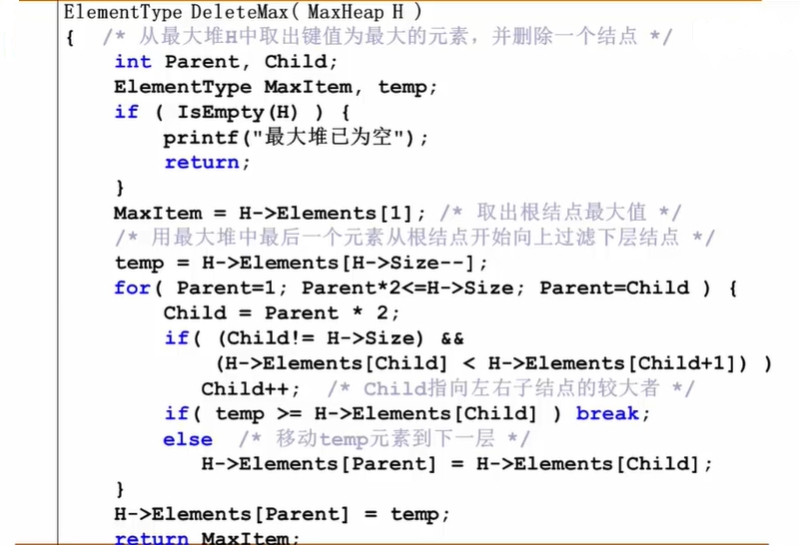
删除

应用创建

如何使用堆排序？ 建立最大堆：将已经存在的N个元素按照最大堆要求存放在一个一维数组中。

方法1：通过插入操作，将N个元素一个个相续插入到一个初始为空的堆中，其中时间代价最大为O(NlogN)

方法2：在线性时间复杂度下建立最大堆，

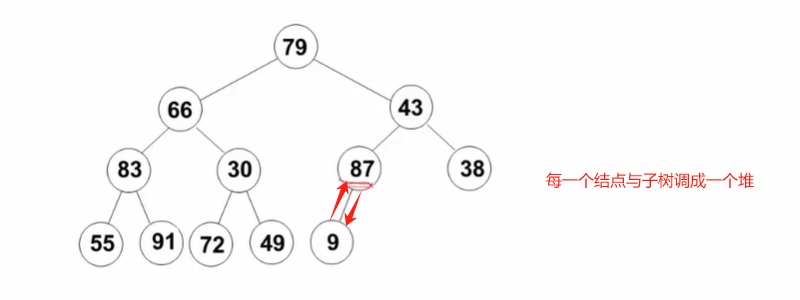
（1）将N个元素按照顺序存入，先满足完全二叉树的结构特性。
（2）再调整各结点位置，以满足最大堆的有序特性。
怎么调整？从倒数第一个开始，从下往上调整