复杂度的渐进表示 ​

T(n) = O(f(n))表示存在常数C > 0，n₀ > 0 使得当 n >= n₀时有T(n) <= C*f(n) 表示的T(n)的某种上界

T(n) = Ω(g(n))表示存在常数C > 0，n₀ > 0 使得当 n >= n₀时有T(n) >= C*g(n) 表示的T(n)的某种下界

T(n) = Θ(h(n))表示同时有T(n) = O(h(n)) 和 T(n) = Ω(h(n)) 既是上界，也是下届，相当于是等价关系

不同复杂度函数的直观表现 ​

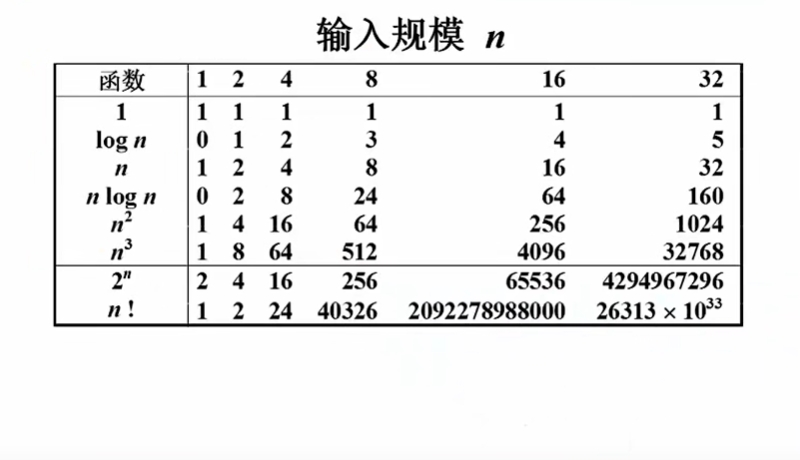
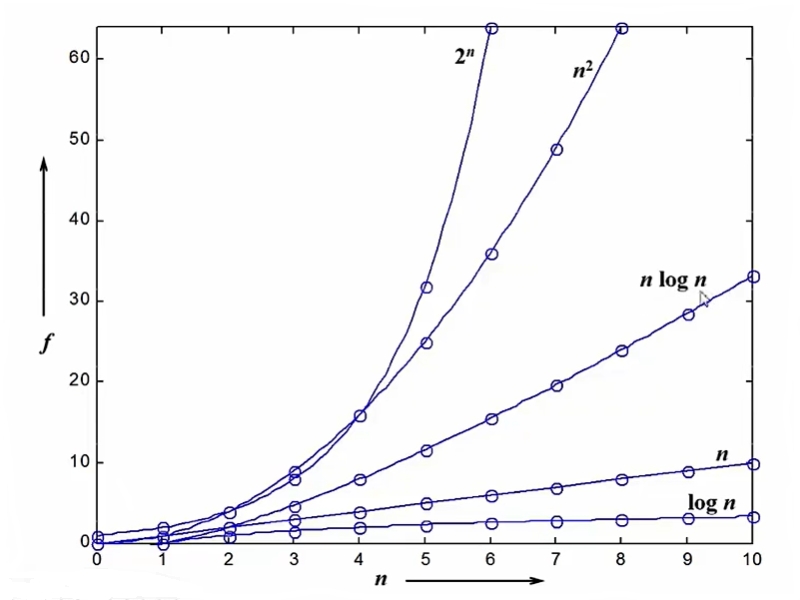
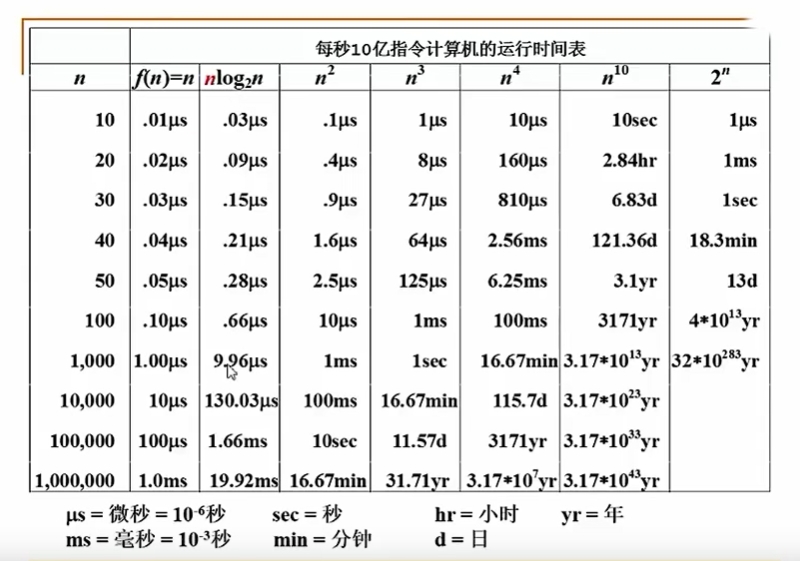
由上图不难看出，log n 是最好的函数

复杂度分析技巧 ​

两段算法分别有复杂度T₁(n) = O(f₁(n)) 和 T₂(n) = O(f₂(n))

• 拼接：T₁(n) + T₂(n) = max(O(f₁(n)) + O(f₂(n)))
• 嵌套：T₁(n) + T₂(n) = O(f₁(n)) * O(f₂(n))

for循环的时间复杂度等于循环次数乘以循环体代码的复杂度。

if-else 结构的复杂度取决于if的条件判断复杂度和两个分支部分的复杂度，总体复杂度取三者中最大的。

复杂度分析 ​

[1,-2,6,-5,6,2,-3,8,-3,4,2,-1]

• 方法一：所有的连续子列和都计算出来 O(n^3)
• 方法二：方法一优化一层 O(n^2)
• 方法三：分而治之 O(n*log n)
• 方法四：在线处理 O(n) （读）