什么是树
示例
数据管理的基础操作查找【示例】
查找:根据某个给定的关键字K,从集合R中找出与关键字K相同的值。
静态查找:集合记录是固定的,没有插入和删除操作,只有查找。(如:查字典)动态查找:集合记录是动态变化的,除了查找,还可能发生删除和插入操作。(如:借图书)
静态查找
静态查找-顺序查找:静态查找,最直接、最简单的方式就是顺序查找。
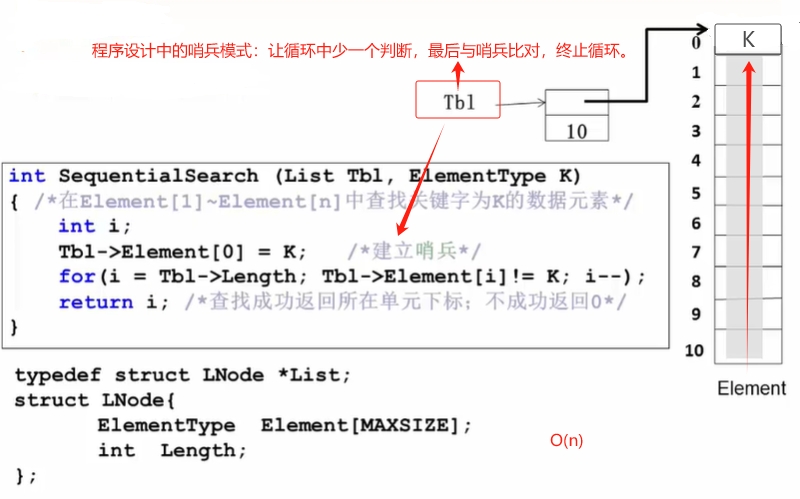
如果数据比较大,`顺序查找`往往不是效率最好的方法。 `二分查找` 的效率要遥遥领先。
静态查找-二分查找:二分查找必须满足,1. 有序,2. 连续存储(数组) 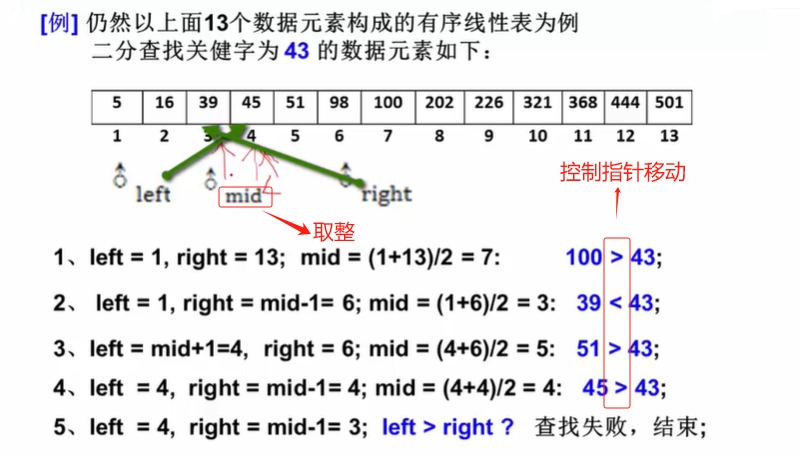 代码实现
代码实现 
分析
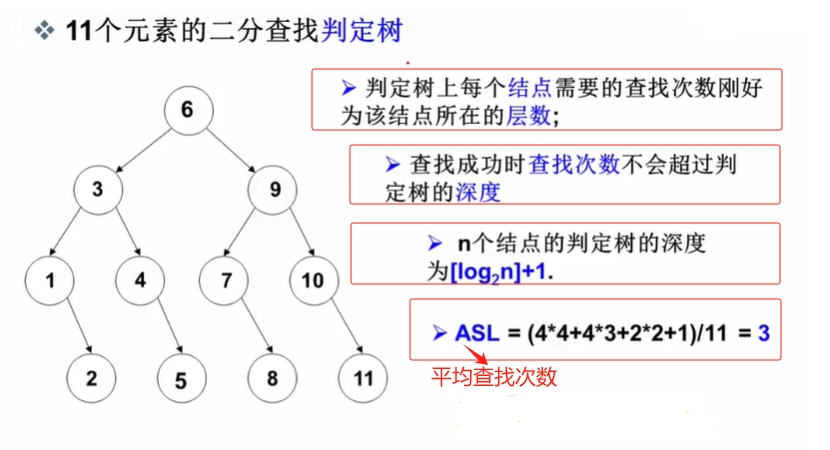
启示
客观的世界中许多事物存在层次关系:
👉人类社会家谱;
👉社会组织结构;
👉图书信息管理;
这些其实都是树结构。分层次组织在管理上具有更高的效率。
那么我们能不能把数据不存放在数组里面呢?我们就按照层次化结构来存数据,是不是也能达到我们想要的效果呢?按照层次化结构来存数据,这就是我们查找树的概念。
- 查找树和二分查找在效率上可以达到相同效果。
- 查找树还可以解决我们另一个问题,
动态查找的问题。
树
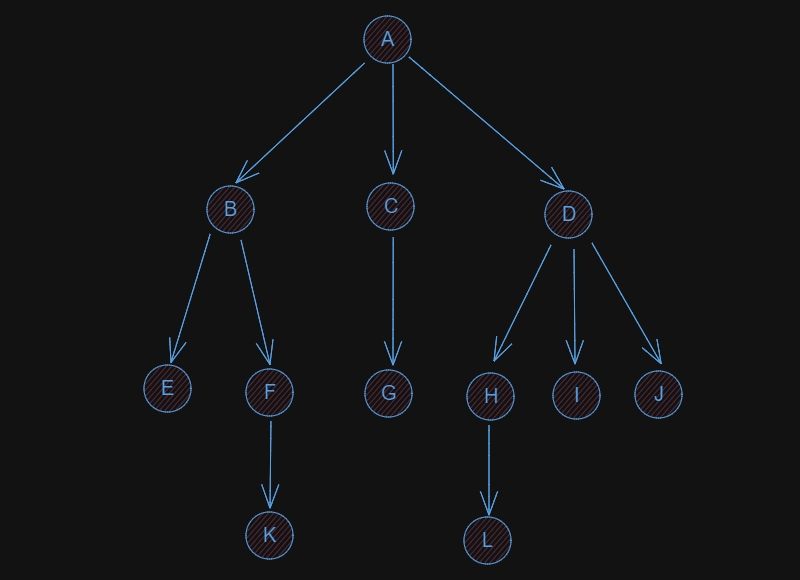
树的定义
树(Tree):n (n >= 0)个节点构成的有限集合。
当n = 0时,称为空树。
当n > 0时,对于一颗非空树,它具备一下性质:
树中有一个特殊结点称为“
根(Root)”,用r表示。其余结点可分为m(m 0 )个
互不相交的有限集T1,T2...Tm,其中每个集合本身又是一颗树,称为原来树的“子树(SubTree)”子树不相交。
每个结点仅且仅有一个父结点(除根结点外)。
一颗N个结点的树有
N-1条边(根结点没有)。
树的术语
结点的度(Degree):结点的子树个数。树的度:树的所有结点中最大的度数。路径:从A到K的路径为一个结点序列A,B,F,K(从上往下)。路径长度:路径所包含边的个数,为路径长度。叶节点(Leaf):度为0的结点。父结点:直接的上下关系结点。子结点:直接的上下关系结点。兄弟结点:拥有同一个父结点。祖先结点:沿着根结点到某一个结点的路径上的所有结点,都是这个结点的祖先结点。子孙结点:某一个结点的子树所有结点,都是这个结点子孙结点。结点的层次(Level):规定根结点在第1层,其他结点是父结点+1。树的深度(Depth):树中所有结点中的最大层次是这颗树的深度。
树的表示
【数组】表示:如果使用数组实现,有些情况会非常麻烦,且对程序设计也不友好。
【链表】表示:如果用链表实现,当结点结构不一致,对后续的程序设计造成负担。
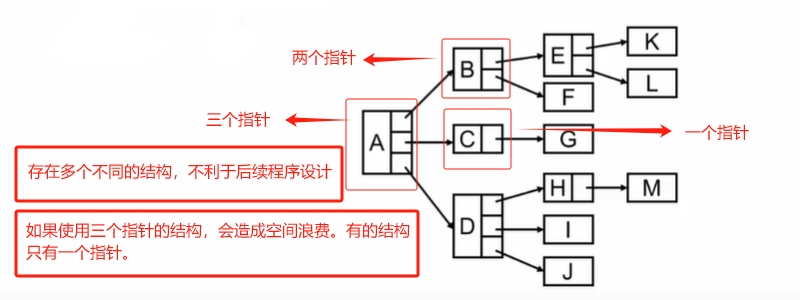
如果使用3n个指针域,我们实际上只有n-1个边。也就是说会有,3n - (n -1)个空指针域,会造成空间浪费。
【儿子-兄弟】表示:在链表的表示基础上做了优化,将每个结点设置成为统一的结构(包含两个指针的结构)。 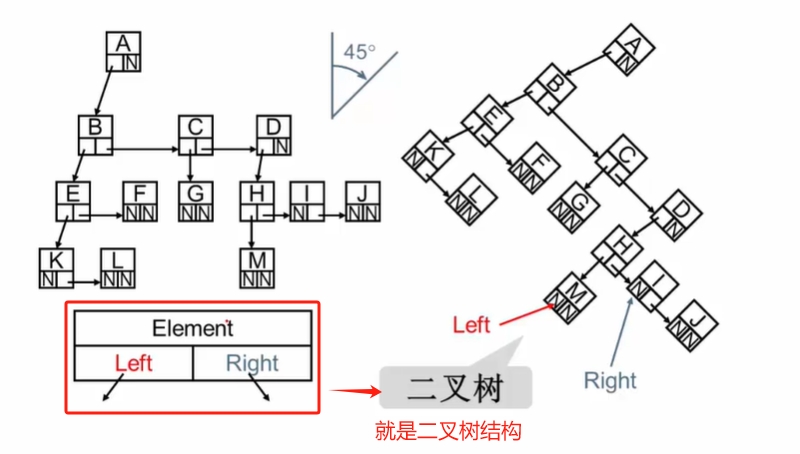
二叉树结构,减少了空间的浪费,同时保证每个结点结构的统一,度为2。
二叉树(T)
二叉树的定义:
一个有穷的结点集合。这个集合可以为空,若不为空,则它由
根结点和称为其左子树TL和右子树TR的两个不相交的二叉树组成。
二叉树基本形态: 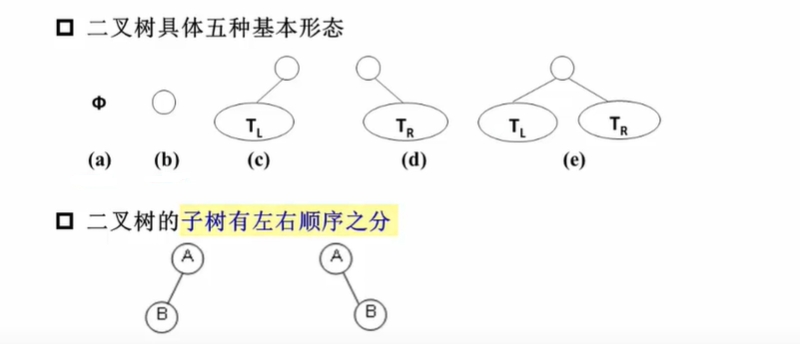
特殊二叉树: 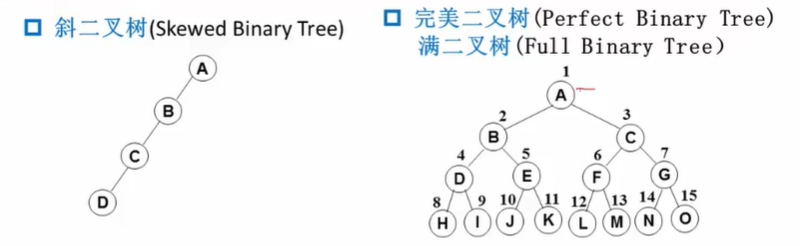
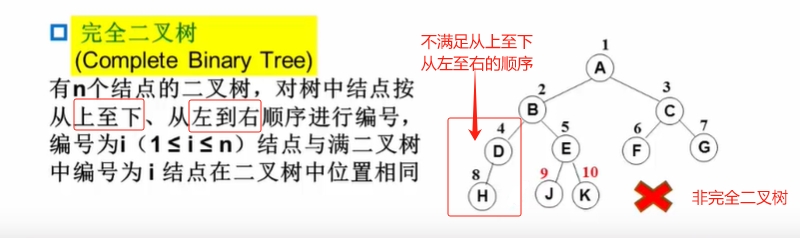
二叉树的几个重要性质:
🟥 一个二叉树第 i 层的最大结点数据为:2i-1,i >= 1。
完美二叉树
🟥 深度为 K 的二叉树的最大结点总数为:2k-1,k >= 1。
1 + 21 + 22 + ... + 2k-1 = 2k - 1
🟥 任何非空二叉树T
若n0表示叶节点,n1表示度为1的结点数,n2表示度为2的结点数。
一定存在 n0 = n2 + 1
二叉树的抽象数据类型描述
抽象数据类型描述
类型名称:二叉树
数据对象集:一个有穷的结点集合,若不为空,则由根结点和其左、右二叉子树组成。
操作集:BT ∈ BinTree,Item ∈ ElementType,重要操作有:
判别BT是否为空。
遍历,按某种顺序访问每一个结点。
创建一个二叉树。
二叉树的遍历
二叉树的遍历非常重要,很多算法设计都是建立在二叉树遍历的基础上的。
先序遍历:根、左子树、右子树;

中序遍历:左子树、根、右子树;

后序遍历:左子树、右子树、根;
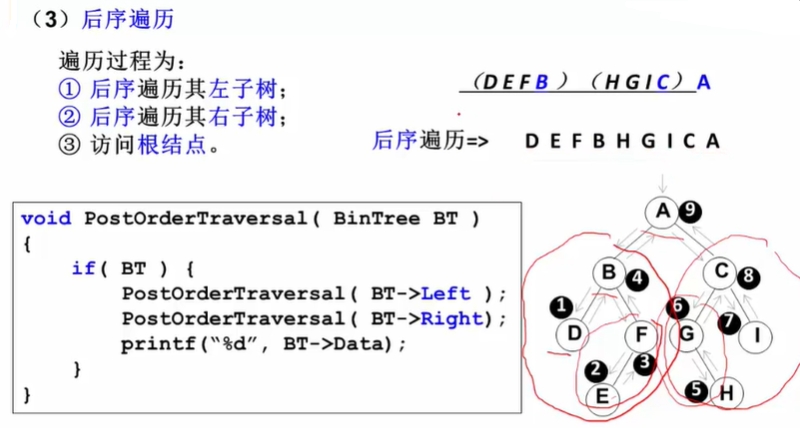
注意
🔴 先序、中序、后序都是基于递归的方法。 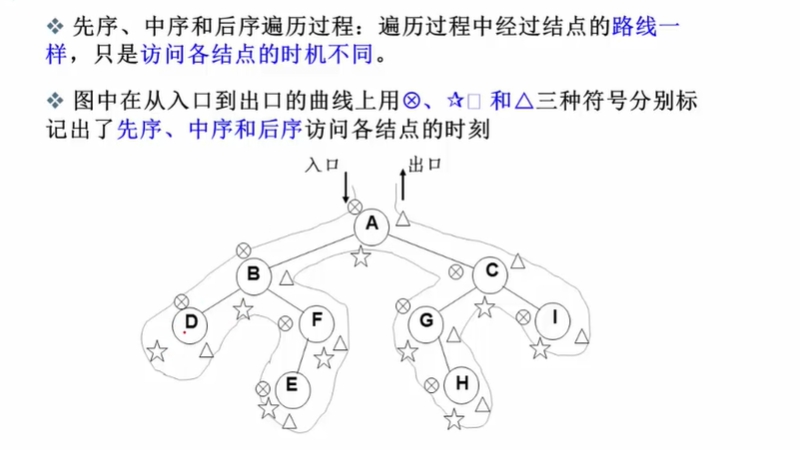
🔴 二叉树的非递归遍历,使用栈。
非递归中序遍历算法【示例】
遇到一个结点,就压入栈中,并去遍历它的左子树。
当左子树遍历结束,从它的栈顶弹除这个结点并访问它。
然后按其右指针再去中序遍历该结点的右子树。
非递归先序、后序遍历算法和非递归中序遍历算法大致一样,应为他们遍历路径是一样的。
层次遍历:从上到下、从左到右;
二叉树遍历的核心问题:将二叉树二维结构的线性化
问题:从结点访问其左、右儿子结点,当访问左儿子结点,右儿子结点(可能有多层)怎么办?
解决:可以使用
栈、队列的储存结构存储暂时不访问的结点。实现:从根结点开始遍历,首先将根结点加入队列。然后执行循环:结点出队,访问该结点,其左右儿子结点加入队列。
代码实现步骤
二叉树的存储
【数组实现二叉树存储】
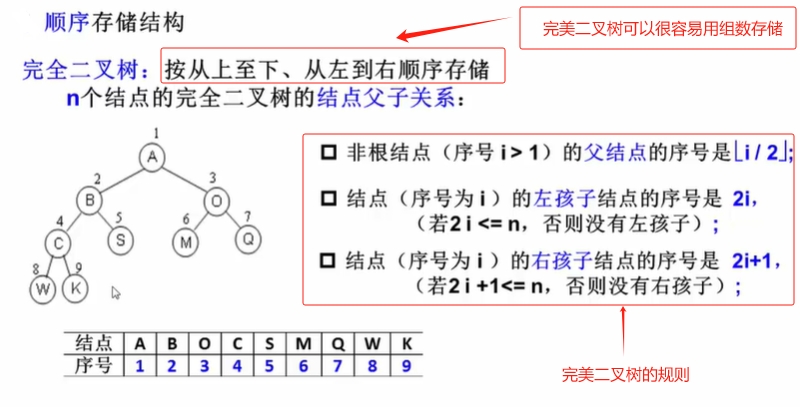
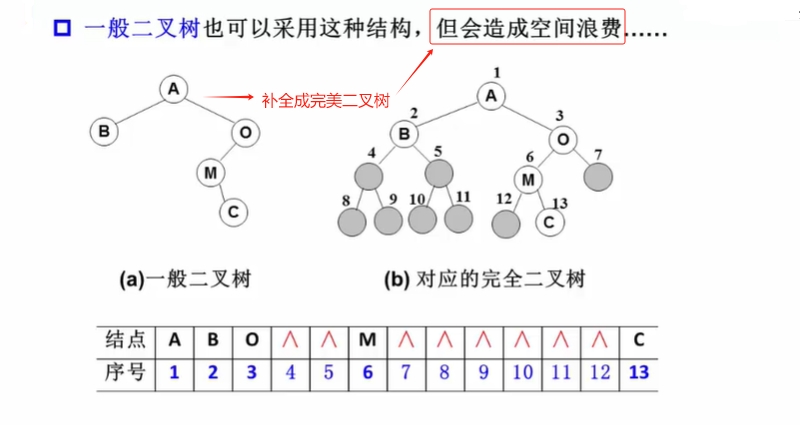
【链表实现二叉树存储】
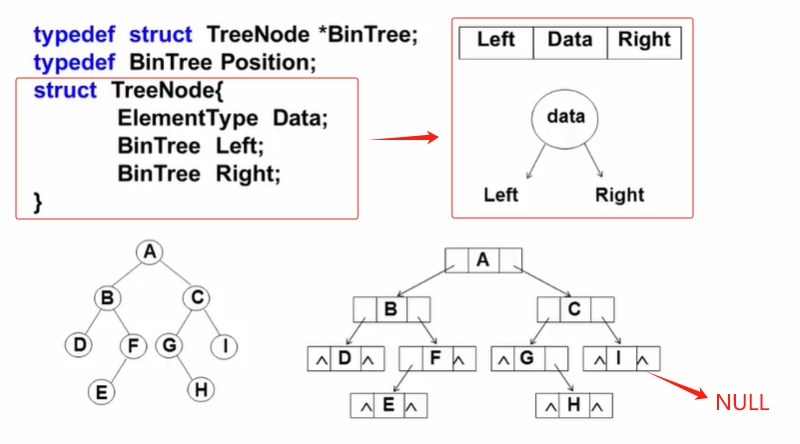
二叉树【题】
- 给定一个二叉树,输出二叉树的中叶子结点。
- 给定一个二叉树,求二叉树的深度。
- 由两种遍历序列确定二叉树。
- 判断同构树。
....
二叉搜索树
二叉搜索树,也称二叉排序树或二叉查找树。可以为空,当不空有以下性质:
🔴 非空左子树的所有键值小于其根结点的键值。
🔴 非空右子树的所有键值大于其根结点的键值。
🔴 左、右子树都是二叉搜索树。

二叉搜索树【查找、插入、删除】
查找
递归实现的效率不高,
尾递归一般都可以使用循环的方式实现。
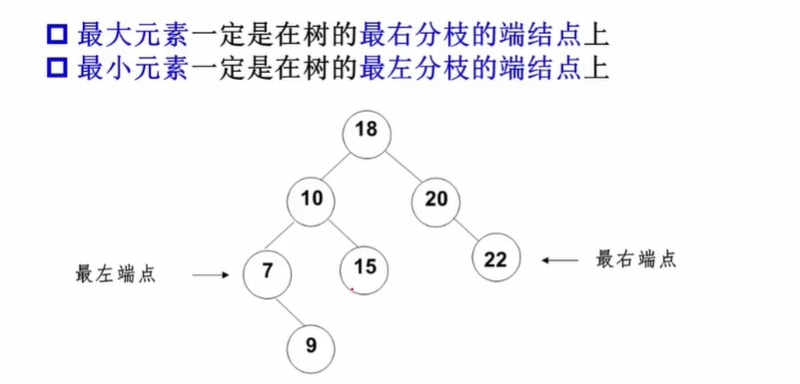
最大值最小值查找
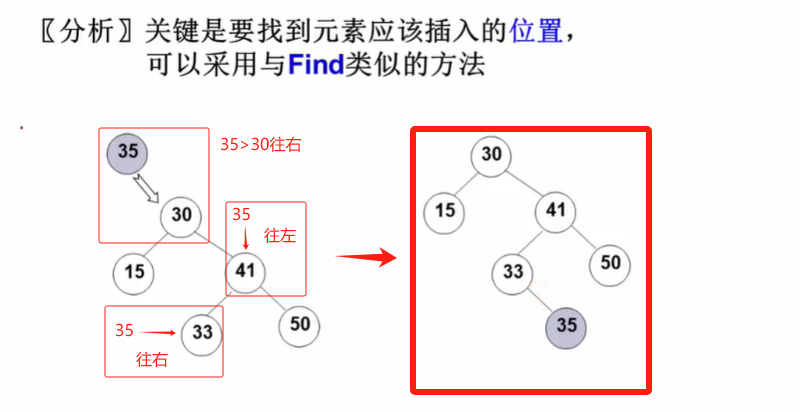
插入
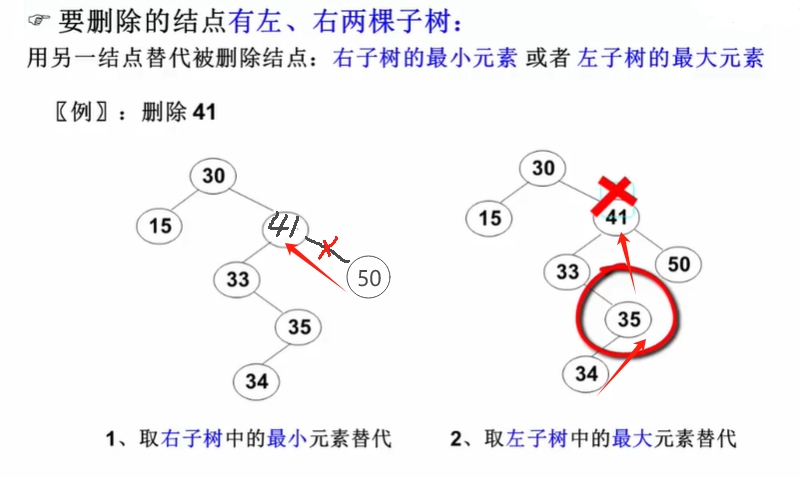
删除
叶节点(只有一个儿子结点):找到后直接删除。
复杂情况:有枝叶结点(多个结点)。
平衡二叉树
什么是平衡二叉树?
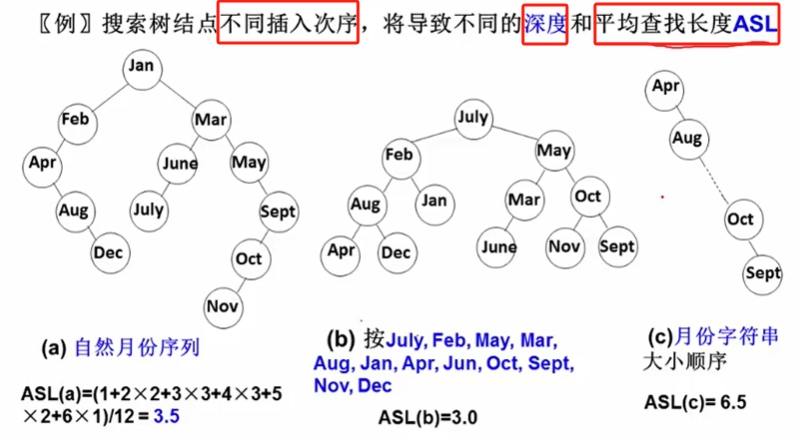
不同的插入次序,会生成不同的二叉树结构,有的查找快,有的查找慢。我们要怎么样设计,才能最优呢?→ 平衡二叉树
平衡二叉树(Balanced Binary Tree)也叫AVL树,在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(logn)。
- 为空时,叫空树。
- 不为空时,任一结点左、右子树
高度差的绝对值不超过1,|BF(T)| <= 1。
BF(T) = hL - hR:
平衡因子(Balance Factor,简称BF),其中hL、hR分别为T的左、右子树的高度。
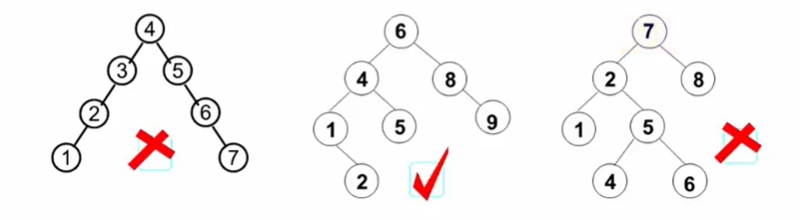
平衡二叉树的高度能达到 log2n 吗?我们所希望的树能够平衡一点,树越平衡高度越低。
拓展
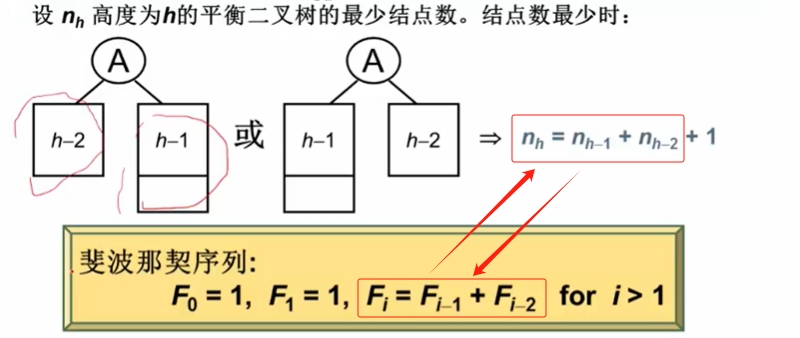

平衡二叉树调整
平衡二叉树调整有四个基本操作
所有的平衡操作都依据被破坏结点(|BF(T)| <= 1 这个不成立时)
RR旋转(左左旋转)
破坏者插入在被破坏者的右子树的右子树上。 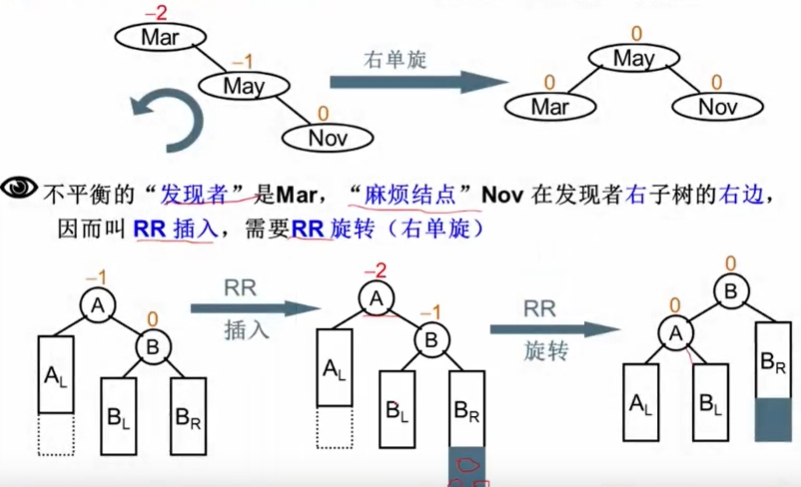
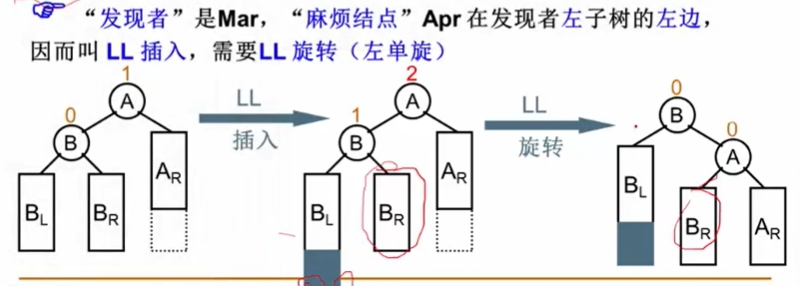
LL旋转(右右旋转)
破坏者插入在被破坏者的左子树的左子树上。 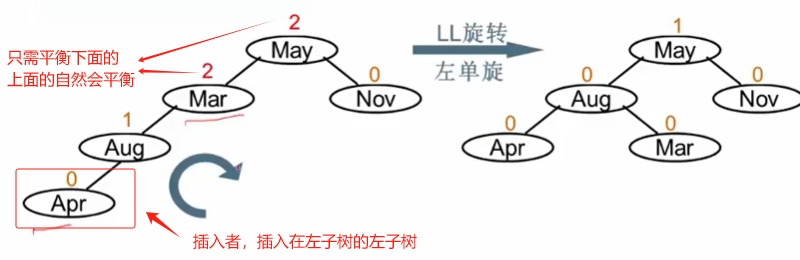
LR旋转(左右旋转)
破坏者插入在被破坏者的左子树的右子树上。 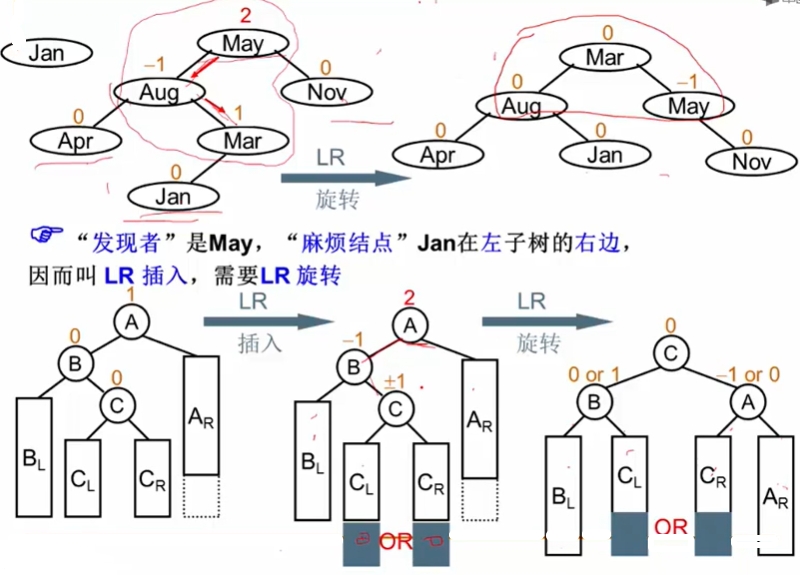
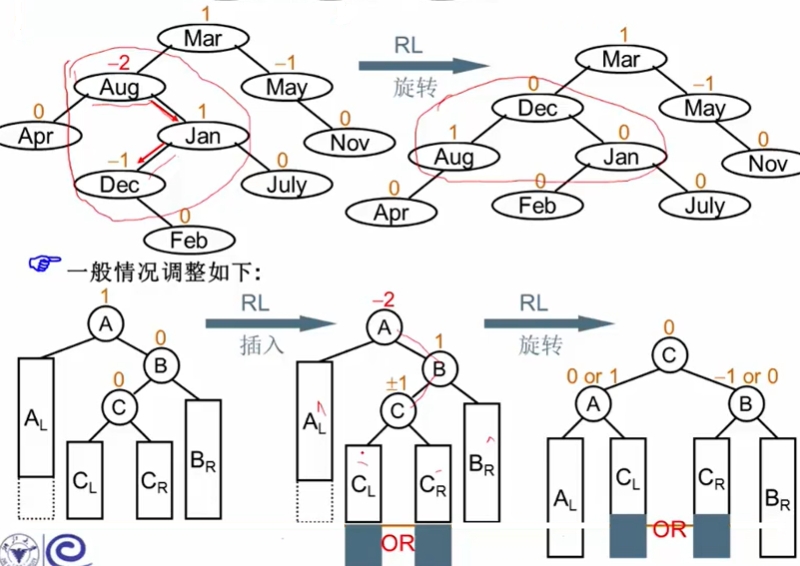
RL旋转(右左旋转)
破坏者插入在被破坏者的右子树的左子树上。