Home

Appearance

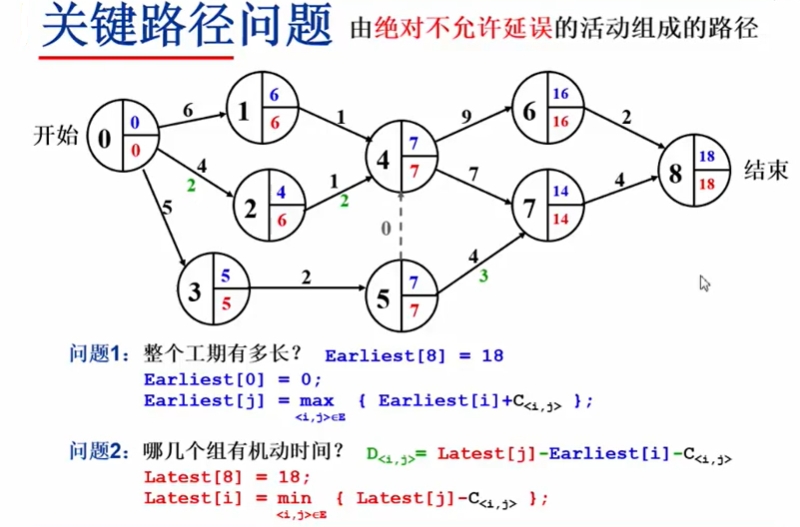
什么是图 ​

【示例】

六度空间理论：你和任何一个不相识的陌生人之间相隔的人数不会超过六个。

村村通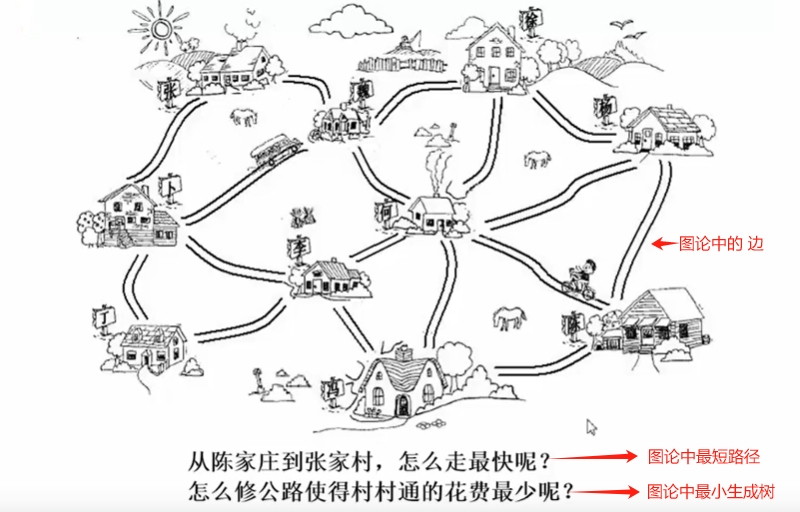： 图片

⭐⭐⭐ 重要 ⭐⭐⭐

线性表是一对一的关系，树是一对多的关系，而图则表示多对多的关系。线性表、树 是图的特殊情况。

图片

抽象数据类型描述 ​

  • 类型名称：图（Graph）；
  • 数据对象集：G（V,E）由一个非空的有限顶点集合 V 和一个有限边集合 E 组成；
  • 操作集：对于任意图 G ∈ Graph，以及 v ∈ V，e ∈ E；

    1. Graph Create()：建立并返回空图；

    2. Graph InsertVertex(Graph G, Vertex V)：将 V 差入 G（插入顶点）；

    3. Graph InsertEdge(Graph G, Edge e)：将 e 插入 G （插入边）；

    4. void DFS(Graph G, Vertex V)：从顶点v出发深度优先遍历图G；

    5. void BFS(Graph G, Vertex V)：从顶点v出发广度优先遍历图G；

    6. void ShortestPath(Graph G, Vertex V, int Dist[])：计算图 G 中顶点 v 到任意其他顶点的最短距离；

    7. void MST(Graph G)：计算图 G 的最小生成树；

    ......

图的术语 ​

  1. 有向图
  2. 无向图
  3. 网络
  4. .......

邻接矩阵【数组表示图】 ​

左边的图 用 矩阵表示 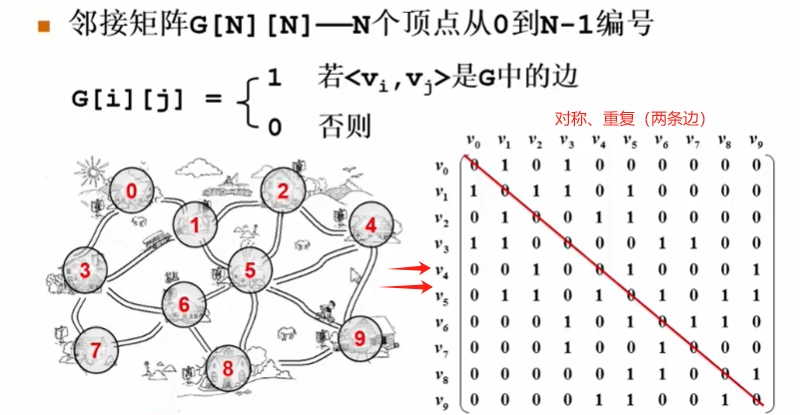图片

存在的问题：对于无向图的存储，怎么样可以省一半的空间？

解决方法：如图 图片

邻接矩阵优点：

  1. 直观、简单、好理解；
  2. 方便检查任意一对顶点间是否存在边；
  3. 方便找任一顶点的所有“邻接点”（有边直接相连的顶点）；
  4. 方便计算任一顶点“度”（从该点发出的边数为“出度”，指向该点的边数为“入度”）；

无向图：对应行（或列），非0元素的个数；

有向图：对应行非0元素的个数是“出度”，对应列非0元素的个数是“入度”；

邻接矩阵缺点：

  1. 浪费空间：对稠密图（完全图）还是很合算的 ，对于稀疏图（点多 边少）有大量无效元素；
  2. 浪费时间：统计稀疏图中一共有多少条边（需要扫描一遍系数图）；

邻阶接表【链表表示图】 ​

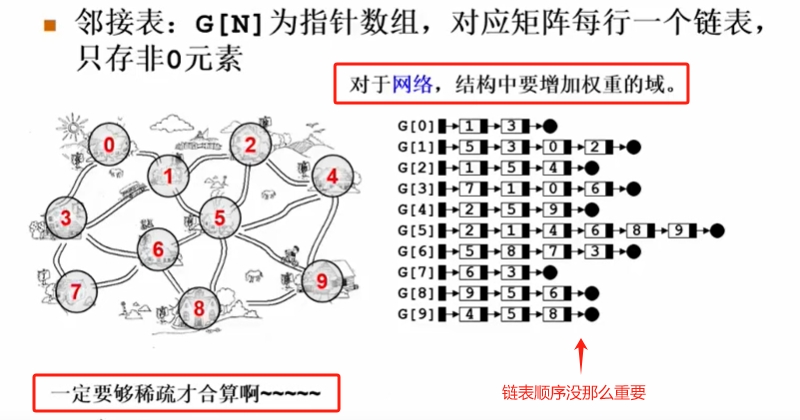图片邻接表优点：

  1. 便找任一顶点的所有“邻接点”；
  2. 节约稀疏图的空间；

需要N个头指针+2E个结点(每个结点至少2个域)

  1. 计算任一顶点的“度”（无向图）方便； 邻接表缺点：
  2. 计算任一顶点的“度”（有向图）困难；

对有向图:只能计算“出度”;需要构造“逆邻接表”(存指向自己的边)来方便计算“入度”

  1. 不方便检查任意一对顶点间是否存在边；

注意

除了邻接矩阵、邻接表，图的表示方式有很多种，如：

  1. 邻接多重表
  2. 十字链表
  3. 边

具体要看解决什么类型的问题。

图的遍历 ​

DFS(深度优先) ​

图片

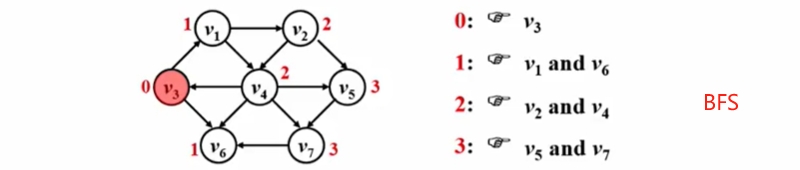
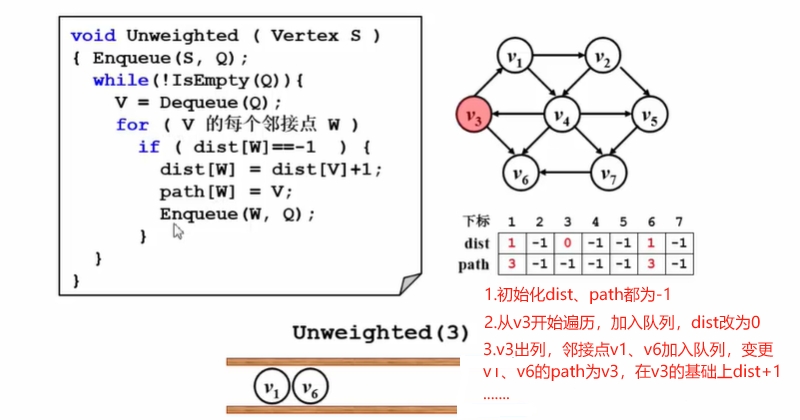
BFS(广度优先) ​

图片



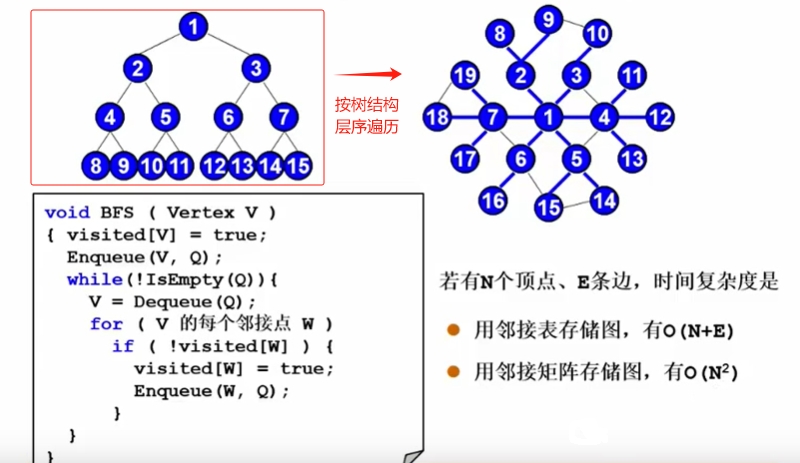
为什么需要这两种遍历方式呢

通过下面示例对比了解（走迷宫）

图片

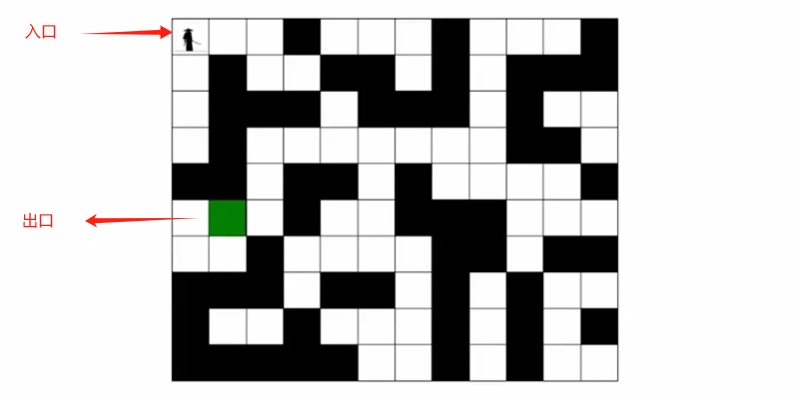
DFS规则:顺时针寻找相邻连接点（当然也可以定其他规则）

⑧①②
⑦🚩③
⑥⑤④

图片

DFS规则: 首先入口进入队列，然后开始把相邻的格子加入队列，一圈一圈的开始遍历搜索。

②②②②②
②①①①②
②①🚩①②
②①①①②
②②②②②

图片

图遍历，是从一个结点出发，沿着边的方向，依次访问图中其它各结点，且每个结点仅被访问一次。

图遍历的一些概念

  1. 连通：如果从V到W存在一条（无向）路径，则称V和W是连通的；

  2. 路径：从顶点V到顶点W存在一系列顶点{V,V1,V2...,W}的集合，其中任一对相邻的顶点间都有图中的边相连接的，

    • 路径长度：是路径中的边数（如果有带权，则是所有边的权重和）；
    • 如果V到W之间的所有顶点都不同，则称简单路径，如果有回路就是不是简单路径；

  3. 回路：从顶点V到顶点V的一条路径；

  4. 连通图：图中任意两个顶点钧连通；

  5. 连通分量：无向图的极大连通子图；

    • 极大顶点数：再加一个顶点就不连通了；
    • 极大边数：包含子图中所有顶点相连的所有边；

    示例

    ABCDEF

  6. 强连通：有向图中顶点v和w之间存在双向路径（V-->W，或者W-->V往返的路径不一定是同一条），则称v和W是强连通的；

  7. 强连通图：有向图中任意两顶点均强连通；

    • 弱连通图：强连通图边的方向抹掉，就是弱连通图；

  8. 强连通分量：有向图的极大强连通子图；

图的算法事例 ​

  1. 拯救007
  2. 六度空间
  3. 哈利波特咒语
  4. ...

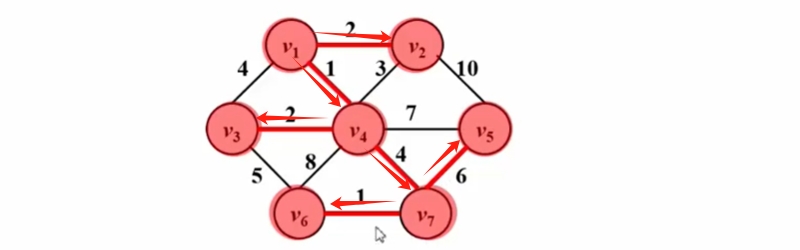
最短路径 ​

生活中从A地点到B地点，花最短时间、花最少的钱 都是图论中的最短路径问题。

最短路径的抽象

在网络中，求两个不同顶点之间的所有路径中，边的权值之和最小的那条路径。

  • 这个路径就是两点之间的最短路径（Shortest Path）；
  • 第一个顶点为源点（Source）；
  • 最后一个顶点为终点（Destination）；

最短路径问题分类

单源最短路径：从固定的某个源点出发：求其到所有其他顶点的最短路径。

无权图（有向/无向）：按照递增（非递减）的顺序找出各个顶点的最短路径；

图片

图片

有权图（有向/无向）：按照递增（非递减）避免负线圈 的顺序找出各个顶点的最短路径；Dijkstra算法用于解决这一问题。

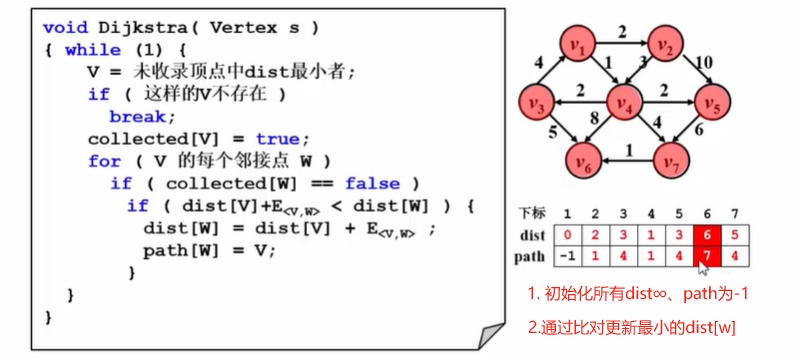
Dijkstra算法

  • 令S = { 源点s + 已经确定了最短路径的顶点Vi }
  • 对于任一未收录的顶点v，定义dist[v]为 s 到 v 的最短路径长度，但该路径仅经过S中的顶点，
    即路径 {s →（ vi ∈ S） → v }的最小长度（ vi ∈ S）是S中的最小路径
  • 路径按照递增（非递减）的顺序生成
  1. 则正真最短路径必须只经过S中的顶点；
  2. 每次从未收录的顶点中选一个dist最小的收录（采用贪心算法策略）；
  3. 增加一个v进入S，可能影响另外一个 w 的dist值；dist[w] = min { dist[w] ， dist[v] + < v ， w >的权重}

Dijkstra算法收录方式：
方法一： 直接扫描所有未收录的顶点 O（|V|），---- 稠密图优势

T=O（|v|2 + |E|）

方法二： 将dist存在最小堆中 O（log|V|）， ---- 稀疏图优势

更新dist[w]的值 O（log|V|）

T=O（|v|log|V| + |E|log|V|）= O（|E|log|V|）

Dijkstra算法实现： 图片


多源最短路径：

方法一：直接将单元最短路径算法调用|V|遍

T=O（|v|3 + |E|*|V|），对于稀疏图比较合算；

方法二：Floyd算法

T=O（|v|3），对于稠密图合算；

Floyd算法

Floyd 算法是一种动态规划算法，基于矩阵运算实现。其思想是通过中间节点逐步优化两个节点之间的距离。首先初始化一个邻接矩阵，其中每一个元素表示两个节点之间的距离，若节点之问没有边，则距离为无穷大。

  • 不是很理解，待补充...

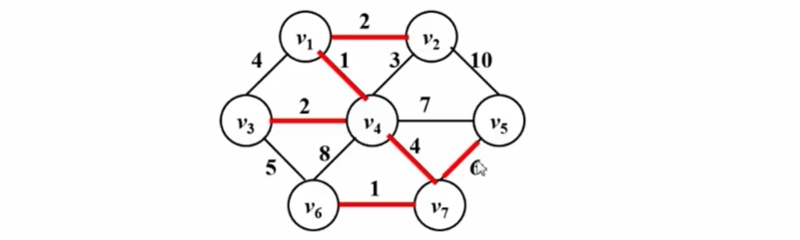
最小生成树 ​

是一颗树：

  • 无回路；
  • |V|个顶点一定有|V|-1条边；

是生成树：

  • 包含全部顶点；
  • |V|-1条边都在图里；
  • 向生成树中任加一条边，都一定构成回路； 图片

边的权重和最小

贪心算法

  • 什么是“贪”：每一步都要最好；

  • 什么是“好”：权重最小的边；

  • 需要约束：

    只能用图里有的边

    只能正好用掉|V|-1条边

    不能有回路


Prim算法（生成最小生成树） ​

图片

图片

Kruskal算法 （将森林合并成树） ​

图片

图片

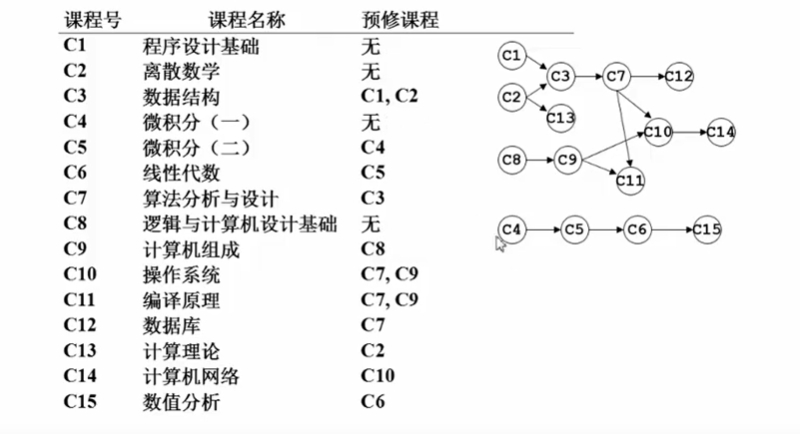
拓扑排序 ​

  • 拓扑序：如果图中从V到W有一条有向路径，则V一定排在W之前。满足次条件的顶点序列称为一个拓扑序；

  • 获得一个拓扑序的过程就是拓扑排序；

  • AOV如果有合理的拓扑序，则必定是有向无环图（Directed Acyclic Graph,DAG）；

图片

图片

关键路径 ​

图片

图片