递归
递归的本质
递归在计算机科学中是指一种通过重复将问题分解为:同类的子类问题而解决问题的方法。
- 递归简单理解:函数调用函数自身。
- 递归本质原理:将问题拆解为更小的子类问题。
- 递归实现逻辑:确定问题、解决基准问题、拆解问题。
Fibonacci
斐波那契:每一项都等于前两项之和
普通计算-递归 Fibonacci
javascript
function fib(n){
if(n <= 1) return n;
return fib(n-1) + fib(n-2)
}
fibonacci(40) // 40 我的电脑需要2s左右 50 浏览器会卡死function fib(n){
if(n <= 1) return n;
return fib(n-1) + fib(n-2)
}
fibonacci(40) // 40 我的电脑需要2s左右 50 浏览器会卡死上面代码展开就是: 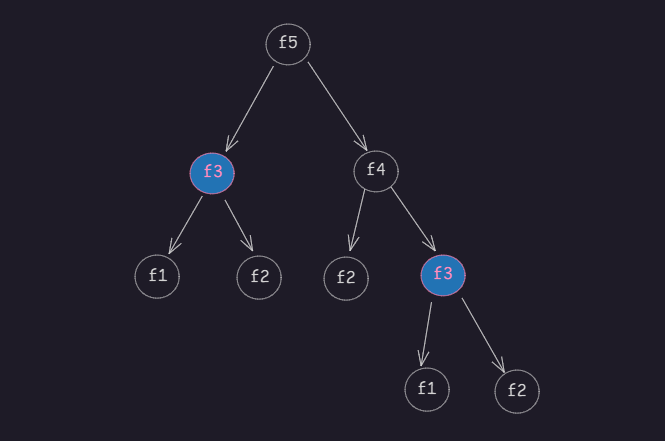
呈现为树形结构。
问题:
斐波那契数列的递归实现通常有性能问题,因为很多子类问题 被重复计算。比如,计算fib(5)时fib(3)会被重复计算,当n 很大时,就有更多的子类问题 被重复计算,程序执行速度会非常慢。间复杂度是 O(2ⁿ)
优化:
想要解决这类有重复计算递归性能问题,可通过**记忆化搜索(Memoization)**优化递归。
- 开一个空数组用于保存第一次的计算结果。下次遇到相同的问题时直接读取。
- 在计算前,先判断这个问题是否有被计算。如没有就直接计算并且保存。如果有就直接读取数组中的结果。
可以将其时间复杂度由指数级的 O(2ⁿ) 降低到 线性的 O(n)。
记忆化搜索-递归
javascript
const memo = [];
function fibonacci(n) {
if (n <= 1) return n;
if (!memo[n]) {
return memo[n] = fibonacci(n-1) + fibonacci(n-2);
}else{
return memo[n]
}
}
fibonacci(100) // 秒出 因为已经从指数级优化成线性。const memo = [];
function fibonacci(n) {
if (n <= 1) return n;
if (!memo[n]) {
return memo[n] = fibonacci(n-1) + fibonacci(n-2);
}else{
return memo[n]
}
}
fibonacci(100) // 秒出 因为已经从指数级优化成线性。循环计算-Fibonacci
javascript
function fibonacci(n) {
let a = 0, b = 1;
for (let i = 2; i <= n; i++) {
[a, b] = [b, a + b];
}
return n === 0 ? a : b;
}function fibonacci(n) {
let a = 0, b = 1;
for (let i = 2; i <= n; i++) {
[a, b] = [b, a + b];
}
return n === 0 ? a : b;
}递归算法-常规应用
- 树形结构遍历
递归天然适合处理树形数据(如 DOM 树、JSON 嵌套)。
javascript
// 递归遍历嵌套对象
function deepFind(obj, targetKey) {
for (const key in obj) {
if (key === targetKey) return obj[key];
if (typeof obj[key] === 'object') {
const res = deepFind(obj[key], targetKey);
if (res !== undefined) return res;
}
}
}// 递归遍历嵌套对象
function deepFind(obj, targetKey) {
for (const key in obj) {
if (key === targetKey) return obj[key];
if (typeof obj[key] === 'object') {
const res = deepFind(obj[key], targetKey);
if (res !== undefined) return res;
}
}
}- 分治算法
将问题分解为多个子问题(如快速排序)。
javascript
function quickSort(arr) {
if (arr.length <= 1) return arr;
const pivot = arr[0];
const left = [], right = [];
for (let i = 1; i < arr.length; i++) {
arr[i] < pivot ? left.push(arr[i]) : right.push(arr[i]);
}
return [...quickSort(left), pivot, ...quickSort(right)];
}function quickSort(arr) {
if (arr.length <= 1) return arr;
const pivot = arr[0];
const left = [], right = [];
for (let i = 1; i < arr.length; i++) {
arr[i] < pivot ? left.push(arr[i]) : right.push(arr[i]);
}
return [...quickSort(left), pivot, ...quickSort(right)];
}- 回溯算法
递归尝试所有可能性(如八皇后问题)。
javascript
// 生成所有括号组合
function generateParenthesis(n) {
const res = [];
function backtrack(str, open, close) {
if (str.length === 2 * n) {
res.push(str);
return;
}
if (open < n) backtrack(str + '(', open + 1, close);
if (close < open) backtrack(str + ')', open, close + 1);
}
backtrack('', 0, 0);
return res;
}// 生成所有括号组合
function generateParenthesis(n) {
const res = [];
function backtrack(str, open, close) {
if (str.length === 2 * n) {
res.push(str);
return;
}
if (open < n) backtrack(str + '(', open + 1, close);
if (close < open) backtrack(str + ')', open, close + 1);
}
backtrack('', 0, 0);
return res;
}递归算法-练习
| 题目 | 难度 | 核心训练点 |
|---|---|---|
| 反转链表 | ⭐️ | 单链表递归操作 |
| 二叉树的最大深度 | ⭐️ | 树形递归 |
| 汉诺塔问题 | ⭐️⭐️ | 分治思想 |
| 全排列 | ⭐️⭐️⭐️ | 回溯算法 |
递归算法-注意
- 栈溢出风险:尾递归可以适当降低调用栈的栈深,递归深度过大(JavaScript 引擎的调用栈深度有限(约 1e4 层)可能导致调用栈溢出,此时应改用迭代法(循环)。
- 记忆化存储:缓存会占用内存,对于极大数值(如 n > 1e5 层)需权衡空间复杂度。